Cache Lab [Updated 5/2/16] (README, Writeup, Release Notes, Self-Study Handout)

At CMU we use this lab in place of the Performance Lab. Students write a general-purpose cache simulator, and then optimize a small matrix transpose kernel to minimize the number of misses on a simulated cache. This lab uses the Valgrind tool to generate address traces.

Note: This lab must be run on a 64-bit x86-64 system.

前言

本篇博客将会介绍 CSAPP 之 CacheLab 的解题过程，分为 Part A 和 Part B 两个部分，其中 Part A 要求使用代码模拟一个高速缓存存储器，Part B 要求优化矩阵的转置运算，此外在介绍正式解题部分前，给出LRU和LFU这两种缓存更新算法的代码。

LRU和LFU缓存更新算法

本实验使用的缓存更新算法为LRU（Least Recently Used），推荐去leetocde上做下LRU和LFU的算法题（面试高频）。

146. LRU Cache

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
struct Node {
  int key, value;
  Node *prev;
  Node *next;
  Node(): key(0), value(0), prev(nullptr), next(nullptr) {}
  Node(int key, int value): key(key), value(value), prev(nullptr), next(nullptr) {}
};

class LRUCache {
private:
  unordered_map<int, Node*> key_table_;
  Node *head_, *tail_;
  int capacity_;

public:
  // must set size_(0), otherwise size_ = -1094795585
  LRUCache(int capacity): capacity_(capacity) {
    head_ = new Node;
    tail_ = new Node;
    head_->next = tail_;
    tail_->prev = head_;
  }
  
  int get(int key) {
    if (!key_table_.count(key)) {
      return -1;
    }
    auto node = key_table_[key];
    moveToHead(node);
    return node->value;
  }
  
  void put(int key, int value) {
    if (!key_table_.count(key)) {
      if (key_table_.size() == capacity_) {
        auto last = tail_->prev;
        removeNode(tail_->prev);
        key_table_.erase(last->key);
        delete last;
      }
      auto node = new Node(key, value);
      addToHead(node);
      key_table_[key] = node;
    } else {
      auto node = key_table_[key];
      node->value = value;
      moveToHead(node);
    }
  }

private:
  void addToHead(Node *node) {
    node->prev = head_;
    node->next = head_->next;
    head_->next->prev = node;
    head_->next = node;
  }

  void removeNode(Node *node) {
    node->prev->next = node->next;
    node->next->prev = node->prev;
    // cannot delete node in removeNode()
    // otherwise moveTohead() will raise heap-use-after-free
  }

  void moveToHead(Node *node) {
    removeNode(node);
    addToHead(node); 
  }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

对比官方题解有两个优点：

  1. 不额外设置size_成员，而使用key_table_.size()，既节约了空间，又减少了直接对size_的操作，降低了犯错风险；
  2. 官方题解中在双向队列满时是先添加再删除，而这里是先删除再添加，更贴合要求。

改进点：没有必要使用head和tail这两个dummy节点，像list[C++11]那样使用双向链表能节约一个节点的空间。

460. LFU Cache

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
struct Node {
  int key, value, freq;
  Node(int key, int value, int freq): key(key), value(value), freq(freq) {};
};

class LFUCache {
private:
  unordered_map<int, list<Node>> freq_table_;
  unordered_map<int, list<Node>::iterator> key_table_;
  int capacity_, min_freq_;

public:
  LFUCache(int capacity): capacity_(capacity), min_freq_(0) {
    // freq_table_.clear();
    // key_table_.clear();
  }
  
  int get(int key) {
    auto it = key_table_.find(key);
    if (it == key_table_.end()) return -1;
    auto node = it->second;
    int value = node->value, freq = node->freq;
    freq_table_[freq].erase(node);
    if (freq_table_[freq].size() == 0) {
      freq_table_.erase(freq);
      if (freq == min_freq_) ++min_freq_;
    }
    freq_table_[freq+1].push_front(Node(key, value, freq+1));
    key_table_[key] = freq_table_[freq+1].begin();
    return value;
  }
  
  void put(int key, int value) {
    auto it = key_table_.find(key);
    if (it == key_table_.end()) {
      if (key_table_.size() == capacity_) {
        auto last = freq_table_[min_freq_].back();  // back()和end()的区别
        freq_table_[min_freq_].pop_back();
        key_table_.erase(last.key);  // 这里是Node
        if (freq_table_[min_freq_].size() == 0) {
          freq_table_.erase(min_freq_);
        }
      }
      freq_table_[1].push_front(Node(key, value, 1));
      key_table_[key] = freq_table_[1].begin();
      min_freq_ = 1;
    } else {
      auto node = it->second;
      int freq = node->freq;
      freq_table_[freq].erase(node);
      if (freq_table_[freq].size() == 0) {
        freq_table_.erase(freq);
        if (freq == min_freq_) ++min_freq_;
      }
      freq_table_[freq+1].push_front(Node(key, value, freq+1));
      key_table_[key] = freq_table_[freq+1].begin();
    }
  }
};

Q: back()和end()的区别？
A: back()返回最后一个元素，end()返回指向最后一个元素的迭代器。

Q: map的迭代方式？
A: 参考https://stackoverflow.com/a/26282004ou can achieve this like following :

1
2
3
4
5
6
7
8
9
map<string, int>::iterator it;

for (it = symbolTable.begin(); it != symbolTable.end(); it++)
{
    std::cout << it->first    // string (key)
              << ':'
              << it->second   // string's value 
              << std::endl;
}

With C++11 ( and onwards ),

1
2
3
4
5
6
7
for (auto const& x : symbolTable)
{
    std::cout << x.first  // string (key)
              << ':' 
              << x.second // string's value 
              << std::endl;
}

With C++17 ( and onwards ),

1
2
3
4
5
6
7
for (auto const& [key, val] : symbolTable)
{
    std::cout << key        // string (key)
              << ':'  
              << val        // string's value
              << std::endl;
}

Part A: Writing a Cache Simulator

Part A 给出了一些后缀名为 trace 的文件，文件中的内容如下图所示，其中每一行代表一次对缓存的操作，格式为 [空格] 操作 地址,数据大小，其中操作的类型有以下几种：

  • I：取指令操作
  • L：读数据操作
  • S：写数据操作
  • M：修改数据操作，比如先读一次数据再写一次数据

只有 I 操作没有带前置空格，其他操作都有一个前置空格。地址为 64 位，数据大小以字节为单位。

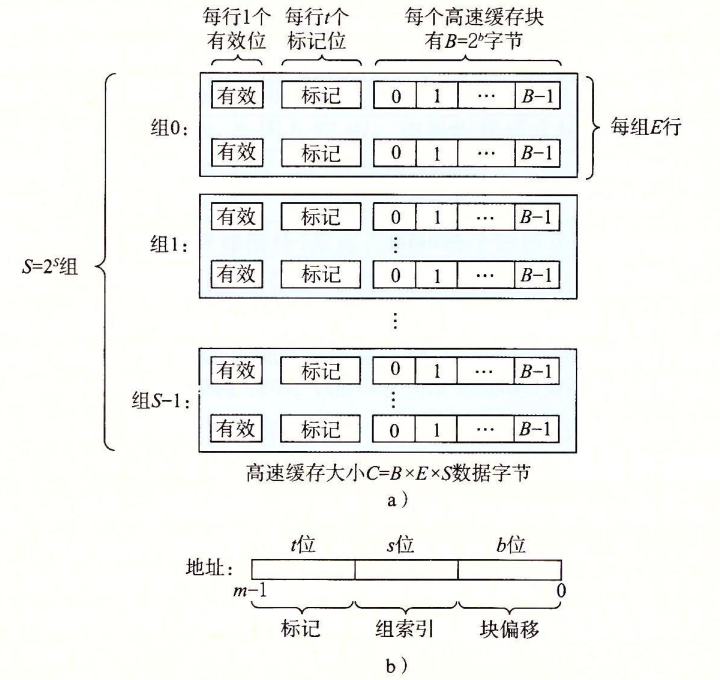
Part A 要求实现的缓存存储器的行为和 csim-ref 一致，使用 LRU 算法进行替换操作。CSAPP 中指出高速缓存存储器可以用四元组 (S,E,B,m)(S,E,B,m) 来描述，其中 S=2sS=2^s 为组数，EE 为行数，B=2bB=2^b 为块的大小，mm 为地址的位数，具体结构如下图所示：

img

对于模拟的高速缓存，至少需要接受 4 个参数：

  • -s：组索引的位数
  • -E：行数
  • -b：块大小 B=2bB=2^b 中的 bb
  • -t：trace 文件的路径

根据给定的 trace 文件，模拟的高速缓存 csim 需要给出命中次数、未命中次数和替换次数，只有和 csim-ref 的次数一样才能拿到分数。

法1：二维数组+计数法

如上，LRU通过实现一个哈希表与双向列表的组合结构，可以实现 put(key) 和 get(key, value) 的时间复杂度均为O(1)O(1)的。
这里使用二维数组+计数模拟时间戳的方法，每次操作后，需要将所有节点的计数都增一，时间复杂度将会达到O(N⋅M)O(N\cdot M)，NN和MM分别表示访问缓存次数和缓存容量大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
#include <assert.h>
#include <getopt.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>

#include "cachelab.h"

typedef struct {
  int valid;  // C中无bool
  int tag;
  int time;
} CacheLine, *CacheSet, **Cache;

void MallocCache();
void FreeCache();
void Simulate();
void LRUUpdate();
void AccessCache(uint64_t addr);

#define MAX_FILE_PATH_LENGTH 100
// C++种可以使用const int类型变量定义数组维度，但是C中不行
// static const int MAX_FILE_PATH_LENGTH = 100;  // error: variably modified
// ‘file_path’ at file scope
static Cache cache;
static int s, S, E, b;
static char file_path[MAX_FILE_PATH_LENGTH];
static int hit, miss, evict;

void MallocCache() {
  cache = (Cache)malloc(S * sizeof(CacheSet));
  assert(cache);
  for (int i = 0; i < S; ++i) {
    cache[i] = (CacheSet)malloc(E * sizeof(CacheLine));
    assert(cache[i]);
    memset(cache[i], 0, sizeof(*cache[i]));
    // memset(cache[i], 0, E * sizeof(CacheLine));
  }
}

void FreeCache() {
  for (int i = 0; i < S; ++i) {
    free(cache[i]);
  }
  free(cache);
}

void Simulate() {
  // 其中 I 和 S 只需访问缓存一次，而 M
  // 需要两次，且每进行一次操作，就得更新一次时间戳：
  FILE *f = fopen(file_path, "r");
  assert(f);
  char op;
  uint64_t addr;  // uint64_t定义在stdint.h中
  int size;
  while (fscanf(f, "%c %lx,%d", &op, &addr, &size) > 0) {  // size 并未使用
    switch (op) {
      case 'M':
        AccessCache(addr);  // 还会往下执行喔
      case 'L':
      case 'S':
        AccessCache(addr);
        break;
    }
    LRUUpdate();
  }
  fclose(f);
}

void LRUUpdate() {
  for (int i = 0; i < S; ++i) {
    for (int j = 0; j < E; ++j) {
      if (cache[i][j].valid) {
        ++cache[i][j].time;
      }
    }
  }
}

void AccessCache(uint64_t addr) {
  int tag = addr >> (b + s);
  uint64_t mask = ((1ULL << 63) - 1) >>
                  (63 - s);  // 低s位1为set需要，高(63+1)-s位0把tag遮掉
  CacheSet cache_set = cache[(addr >> b) & mask];

  // 有命中
  for (int i = 0; i < E; ++i) {
    if (cache_set[i].valid && cache_set[i].tag == tag) {
      ++hit;
      cache_set[i].time = 0;
      return;
    }
  }
  ++miss;

  // 有空位，直接写入
  for (int i = 0; i < E; ++i) {
    if (!cache_set[i].valid) {
      cache_set[i].valid = 1;
      cache_set[i].tag = tag;
      cache_set[i].time = 0;
      return;
    }
  }

  // 没有空位，只能使用LRU算法进行替换
  ++evict;
  int evict_idx = 0, max_time = 0;
  for (int i = 0; i < E; ++i) {
    if (cache_set[i].time > max_time) {
      max_time = cache_set[i].time;
      evict_idx = i;
    }
  }
  cache_set[evict_idx].tag = tag;
  cache_set[evict_idx].time = 0;
}

int main(int argc, char *argv[]) {
  int opt;
  while ((opt = getopt(argc, argv, "s:E:b:t:")) !=
         -1) {  // 't'后面也要加':'，否则会报segmentation fault
    switch (opt) {
      case 's':
        s = atoi(optarg);
        S = 1 << s;
        break;
      case 'E':
        E = atoi(optarg);
        break;
      case 'b':
        b = atoi(optarg);
        break;
      case 't':
        strcpy(file_path, optarg);
        break;
    }
  }
  MallocCache();
  Simulate();
  FreeCache();

  printSummary(hit, miss, evict);
  return 0;
}

法2：双向链表

感觉二维数组其实比双向链表更贴合缓存的硬件实现，但是散列表+双向链表更适合软件实现缓存更新算法，下面的实现中并未使用散列表。二维数组模拟表示中需要使用valid字段，但是双向链表中不需要：链表中所有元素都是合法的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
#include <assert.h>
#include <getopt.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>

#include "cachelab.h"

typedef struct _Node {
  // unsigned valid;  // 使用链表模拟CacheLine就不需要valid了
  uint64_t tag;
  struct _Node *prev;
  struct _Node *next;
} Node;

typedef struct {
  Node *head;
  Node *tail;
  int *size;  // 好像不用int*, 用int确实不太行
} LRUCacheSet;

void InitializeLRU(int i);
void Simulate();
void Update(uint64_t addr);
void DeleteElement(LRUCacheSet *cur_set, Node *node);
void AddToHead(LRUCacheSet *cur_set, Node *node);
void MoveToHead(LRUCacheSet *cur_set, Node *node);

static LRUCacheSet *cache;
#define MAX_FILE_PATH_LENGTH 100
static int s, S, E, b;
static char file_path[MAX_FILE_PATH_LENGTH];
static int hit, miss, evict;

void InitializeLRU(int i) {
  cache[i].head = malloc(sizeof(Node));
  cache[i].tail = malloc(sizeof(Node));
  cache[i].head->next = cache[i].tail;
  cache[i].tail->prev = cache[i].head;
  cache[i].size = malloc(sizeof(int));
  *(cache[i].size) = 0;
}

void Simulate() {
  cache = malloc(S * sizeof(LRUCacheSet));
  for (int i = 0; i < S; ++i) {
    InitializeLRU(i);
  }
  // 其中 I 和 S 只需访问缓存一次，而 M
  // 需要两次，且每进行一次操作，就得更新一次时间戳：
  FILE *f = fopen(file_path, "r");
  assert(f);
  char op;
  uint64_t addr;  // uint64_t定义在stdint.h中？
  int size;
  while (fscanf(f, "%c %lx,%d", &op, &addr, &size) > 0) {  // size 并未使用
    switch (op) {
      case 'M':
        Update(addr);
      case 'L':
      case 'S':
        Update(addr);
        break;
    }
  }
  fclose(f);
}

void Update(uint64_t addr) {
  uint64_t tag = addr >> (b + s);
  uint64_t mask = ((1ULL << 63) - 1) >> (63 - s);
  LRUCacheSet target_cache_set = cache[(addr >> b) & mask];
  Node *cur = target_cache_set.head->next;
  // 以下使用顺序查找的方式，而非上述算法题中hash映射法,
  // 也非硬件采取的快速查抄（猜硬件不会遍历）
  int found = 0;
  while (cur != target_cache_set.tail) {
    if (cur->tag == tag) {
      found = 1;
      break;
    }
    cur = cur->next;
  }
  if (!found) {
    ++miss;
    Node *new_node = malloc(sizeof(Node));
    new_node->tag = tag;
    if (*(target_cache_set.size) == E) {
      DeleteElement(&target_cache_set, target_cache_set.tail->prev);
      // free(target_cache_set.tail->prev);
      ++evict;
    }
    AddToHead(&target_cache_set, new_node);
  } else {
    ++hit;
    MoveToHead(&target_cache_set, cur);
  }
}

void DeleteElement(LRUCacheSet *cur_set, Node *node) {
  node->next->prev = node->prev;
  node->prev->next = node->next;
  --*(cur_set->size);
}

void AddToHead(LRUCacheSet *cur_set, Node *node) {
  node->prev = cur_set->head;
  node->next = cur_set->head->next;
  cur_set->head->next->prev = node;
  cur_set->head->next = node;
  ++*(cur_set->size);
}

void MoveToHead(LRUCacheSet *cur_set, Node *node) {
  DeleteElement(cur_set, node);
  AddToHead(cur_set, node);
}

int main(int argc, char *argv[]) {
  int opt;
  while ((opt = getopt(argc, argv, "s:E:b:t:")) !=
         -1) {  // 't'后面也要加':'，否则会报segmentation fault
    switch (opt) {
      case 's':
        s = atoi(optarg);
        S = 1 << s;
        break;  // 需要break吗?
      case 'E':
        E = atoi(optarg);
        break;
      case 'b':
        b = atoi(optarg);
        break;
      case 't':
        strcpy(file_path, optarg);
        break;
    }
  }
  Simulate();
  printSummary(hit, miss, evict);
  return 0;
}

[problems]对于以上代码，个人有两点困惑：

  1. 为什么第21行中int *size 必须使用int*而不能是int？
    郭郭wg 2:38 说是为了永久化修改，否则后期可能会发现值并未修改。
    可我还是没有搞懂。
  2. 为什么89行中的free(target_cache_set.tail->prev)不能加上？
    删除后会导致Error running test simulator: Status 139, 实在是没理解为啥会这样。个人猜测是对free()的理解还不到位。

如果大佬能解答我的困惑，若能在评论区不吝赐教，本人将不胜感激！

Part B: Optimizing Matrix Transpose

题目要求在trans.c中编写矩阵转置的函数，在一个 s = 5, E = 1, b = 5 的缓存中进行读写，针对 32×3232×32、64×6464×64和 61×6761×67 这三种维度的矩阵进行优化，最多使用12个局部变量。同时给出了以下两点友情提示：

  • 使用分块技术进行优化
  • 对角线上的元素会引发冲突未击中

原始转置代码中的问题——为什么要分块

s = 5, E = 1, b = 5 的缓存有32组，每组一行，每行存 8 个int。Part B 给出了最原始的转置操作代码：

1
2
3
4
5
6
7
8
9
10
void trans(int M, int N, int A[N][M], int B[M][N]) {
    int i, j, tmp;

    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    }
}

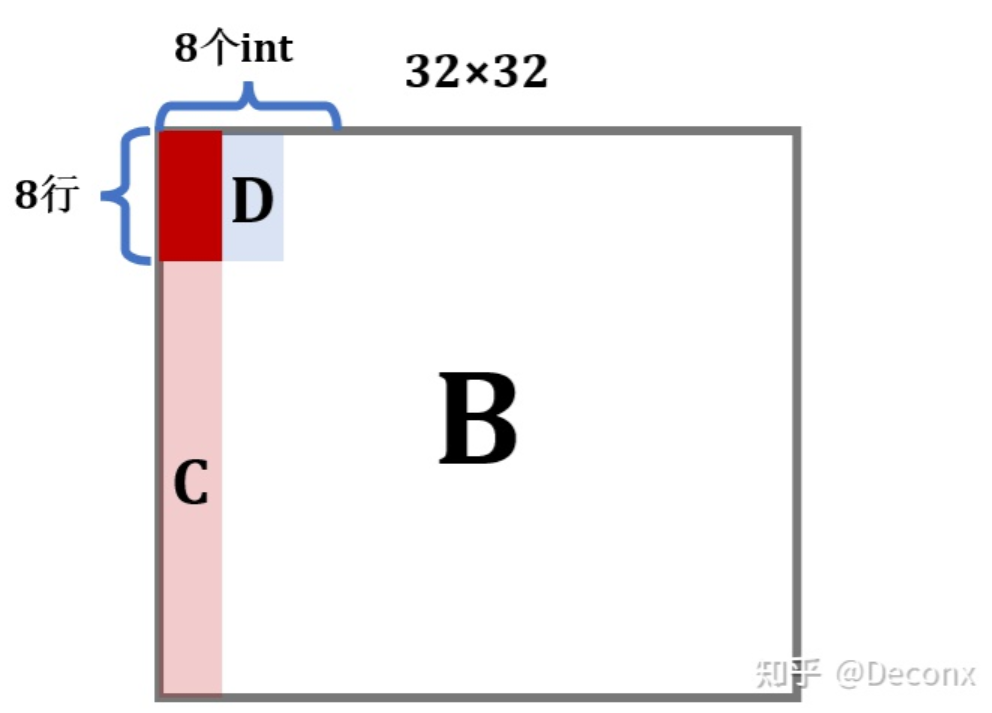
由于C语言中矩阵是行优先存储的，因此对于A矩阵来说，代码是缓存友好的：在从内存读 A[0][0] 的时候，除了 A[0][0] 被加载到缓存中，它之后的 A[0][1]---A[0][7] 也会被加载进缓存。但对于B矩阵而言，写入B矩阵是一列一列写入的：

在写入B的前 8 行后，B的D区域就全部进入了缓存，此时如果能对D进行操作，那么就能利用上缓存的内容，不会miss；但是，暴力解法接下来操作的是C，每一个元素的写都要驱逐之前的缓存区，当来到第 2 列继续写D时，它对应的缓存行很可能已经被驱逐了，于是又要miss，也就是说，暴力解法的问题在于没有充分利用上已经进入缓存的元素。

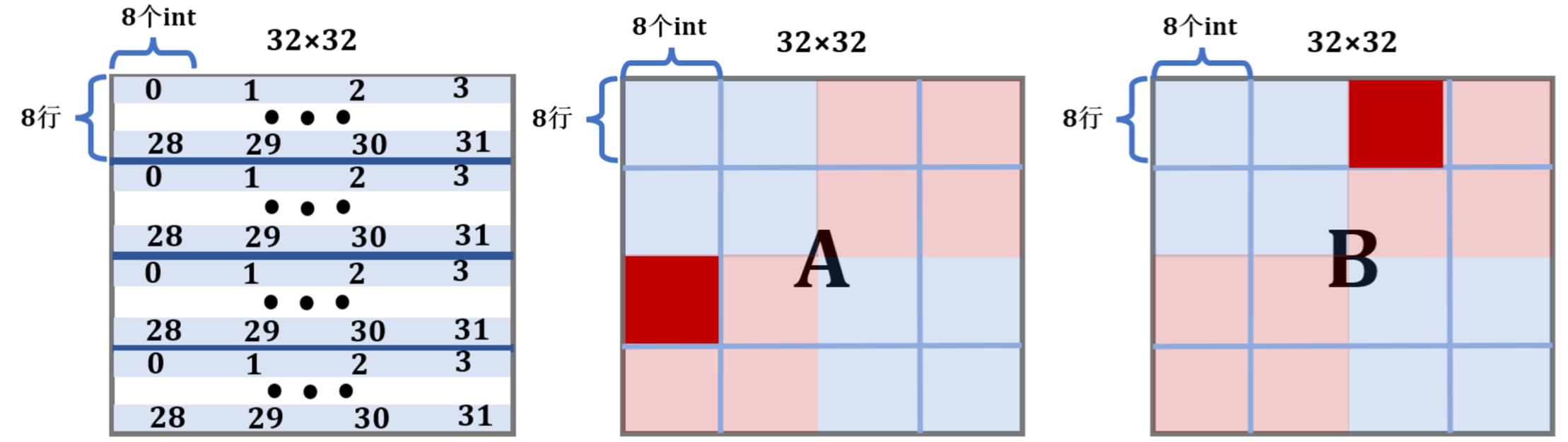
缓存只够存储一个矩阵的四分之一（宽度为1/4，面积为1/16），A中的元素对应的缓存行每隔8行就会重复。A和B的地址由于取余关系（可见源码中矩阵定义或实验材料中暗示），每个元素对应的地址是相同的。各个元素对应缓存行如下左图：

image-20231003210854911

32×32

分块解决的是在矩阵转置过程中，两个矩阵的内存的访问顺序不同导致的缓存不友好的问题，其缓解了同一个矩阵内部缓存块相互替换的问题。

分块的单位一般是一个经验值，比如我们从这道题入手分析，发现A矩阵从第9行开始出现了缓存冲突，因此可以使用 8×88\times 8 的分块技术（因为在 8×88\times 8 的分块内，不存在矩阵内部的缓存冲突）。

如上一张图右图所示，结合左图中块标号来看，A中标红的块占用的是缓存的第 0，4，8，12，16，20，24，28组，而B中标红的块占用的是缓存的第2，6，10，14，18，16，30组，刚好不会冲突（虽然这样浪费了奇数序号的缓存行）。事实上，除了对角线，A与B中对应的块都不会冲突。

1
2
3
4
5
for (int i = 0; i < N; i += 8)
    for (int j = 0; j < M; j += 8)
        for (int i1 = i; i1 < i + 8; ++i1)
            for (int j1 = j; j1 < j + 8; ++j1)
                B[j1][i1] = A[i1][j1];

测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(base) ➜  l4_cachelab ./test-trans -M 32 -N 32    

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:1709, misses:344, evictions:312

Function 1 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 1 (Simple row-wise scan transpose): hits:869, misses:1184, evictions:1152

Summary for official submission (func 0): correctness=1 misses=344

TEST_TRANS_RESULTS=1:344

Function 0对应上述代码，Function1对应题目给出的原始代码。二者的缓存不命中次数结果分别为344和1184。

  • Function 0的理论分析：对于A中每一个操作块，只有每一行的第一个元素会不命中，所以为8次不命中；对于B中每一个操作块，只有每一列的第一个元素会不命中，所以也为 8 次不命中。总共miss次数为：8 × 16 × 2 = 256。

  • Function 1的理论分析：对于A，每8个int就会占满缓存的一组，所以每一行会有 32/8 = 4 次不命中；而对于B，考虑最坏情况，每一列都有 32 次不命中，由此，算出总不命中次数为 4 × 32 + 32 × 32 = 1152。

可以观察到二者结果均比理论值要多一些，而理论上这个数应该小于等于理论分析结果。出现这一偏差的原因就在于：对角线上的缓冲块会冲突。

使用局部变量缓解对角线冲突：原理

困惑与感悟：

困惑：之前作者一直有个疑惑：为什么把内存读入到缓存中，不能直接写到其他内存？

感悟：
要搞清楚tag到底是什么，如下图：

image-20231003220409021

tag是地址的第一部分，是内存地址的一部分，A和B两个矩阵这部分tag是不同的。

不存在直接从内存到内存的指令（这样会大大降低CPU时钟频率)，也不存在缓存到缓存到缓存的指令。因此读时是从内存到缓存再到CPU，而写时是从CPU到缓存再到内存，就算对于A[0]=B[0]这样的代码而言，也是不能把B[0]读入到缓存再把这块代码写给A[0]对应内存的——二者虽然index和offset都相同，但是tag不同，不能乱搞喔（电路上tag会不匹配）！

在仅进行 8×88\times 8分块时，缓存替换情况如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
缓存中的内容 :
+-----------------------+-------------------+
| opt                   |  cache            |
+-----------------------+-------------------+
|before B[0][0]=tmp     | A[0]              |---+
+-----------------------+-------------------+   |
|after B[0][0]=tmp      | B[0]              |   |    
+-----------------------+-------------------+   |    A 的第一行复制到 B 的第一列.
|after tmp=A[0][1]      | A[0]              |   |    最终缓存中剩下 A[0], B[1]...B[7].
+-----------------------+-------------------+   +--> A[0]被两次加载进入内存, 
|after B[1][0]=tmp      | A[0] B[1]         |   |    总的 miss 次数是 10.               
+-----------------------+-------------------+   |    
|...                    |                   |   |    
+-----------------------+-------------------+   |
|after B[7][0]=tmp      | A[0] B[1..7]      |---+
+-----------------------+-------------------+
|after B[0][1]=tmp      | A[1] B[0] B[2..7] |---+
+-----------------------+-------------------+   |    A 的第二行复制到 B 的第二列.
|after B[1][1]=tmp      | B[0..7]           |   |    其中发生的 miss 有 : 
+-----------------------+-------------------+   +--> A[0], B[0], A[1]与 B[1]的相互取代. 
|after B[2][1]=tmp      | A[1] B[0] B[2..7] |   |    总的 miss 次数为 4.
+-----------------------+-------------------+   |
|...                    |                   |   |    
+-----------------------+-------------------+   |
|after B[7][1]=tmp      | A[1] B[0] B[2..]  |---+
+-----------------------+-------------------+        之后的三至七行与第二行类似,
|...                    |                   |------> miss 的次数都是 4.
+-----------------------+-------------------+
|after tmp=A[7][7]      | A[7] B[0..6]      |---+    最后一行 A[7] 被 A[8]取代后,
+-----------------------+-------------------+   +--> 不需要重新加载 .
|after B[7][7]=tmp      | B[0..7]           |---+    总的 miss 数为 3. 
+-----------------------+-------------------+

所以对角块上的总的 miss 次数是 10+4*6+3=37.

分析：

  • 第5行tmp在这里指的不是某个变量，而是未命名的缓存集（cache set），在 before B[0][0]=tmp 时需要把A[0]读入缓存赋给cache。

  • 第7行A[0]被B[0]驱逐是因为二者映射到了同一位置，注意第7行A[0]被B[0]驱逐，随后第9行B[0]又被A[0]驱逐：B[1][0]需要使用A[0][1] 。

  • 第17行在after B[0][1]=tmp时A[1]会miss，在after B[0][1]=tmp时B[0]会miss，而后第19行B[1]会miss，而21行时A[1]会miss。

  • 对角分块有 4 个，普通的分块 12 个，所以总的 miss 数是 4×37+12×8×2=3404\times 37+12\times 8\times 2=340，和实际结果相差 4。4 是一个固定的偏差， 程序可能在这个过程中有 4 次额外的内存访问，在后面的根据算法定量分析结果和实际结果中都会有 4 次 miss 的偏差。

使用局部变量的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int a0, a1, a2, a3, a4, a5, a6, a7;
for (int i = 0; i < 32; i += 8) {
    for (int j = 0; j < 32; j += 8) {
        for (int k = i; k < i + 8; k++) {
            a0 = A[k][j];
            a1 = A[k][j + 1];
            a2 = A[k][j + 2];
            a3 = A[k][j + 3];
            a4 = A[k][j + 4];
            a5 = A[k][j + 5];
            a6 = A[k][j + 6];
            a7 = A[k][j + 7];
            B[j][k] = a0;
            B[j + 1][k] = a1;
            B[j + 2][k] = a2;
            B[j + 3][k] = a3;
            B[j + 4][k] = a4;
            B[j + 5][k] = a5;
            B[j + 6][k] = a6;
            B[j + 7][k] = a7;
        }
    }
}

注意：a0…a7一定要写在函数体内，不能写在函数外，否则缓存hit和miss的次数都会大大增加。
个人不是很理解：放在栈和放在堆上不都是放在内存，放在DRAM中吗？

缓存替换情况如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
缓存中的内容 :
+-----------------------+-------------------+
| opt                   |  cache            |
+-----------------------+-------------------+
|after tmp=A[0][0]      | A[0]              |
+-----------------------+-------------------+
|after tmp=A[0][1]      | A[0]              |
+-----------------------+-------------------+
|after tmp=A[0][2]      | A[0]              |
+-----------------------+-------------------+
|...                    |                   |
+-----------------------+-------------------+
|after tmp=A[0][7]      | A[0]              |
+-----------------------+-------------------|
|after B[0][0]=tmp      | B[0]              | ---> 缓存替换
+-----------------------+-------------------+
|after B[1][0]=tmp      | B[0..1]           |
+-----------------------+-------------------+
|after B[2][0]=tmp      | B[0..2]           |
+-----------------------+-------------------+
|...                    |                   |
+-----------------------+-------------------+
|after B[7][0]=tmp      | B[0..7]           |
+-----------------------+-------------------+
|after tmp=A[1][0]      | A[1] B[0] B[2..7] | ---> 缓存替换
+-----------------------+-------------------+
|...                    |                   |
+-----------------------+-------------------+
|after tmp=A[1][7]      | A[1] B[0] B[2..7] |
+-----------------------+-------------------+
|after B[0][1]=tmp      | A[1] B[0] B[2..7] |
+-----------------------+-------------------+
|after B[1][1]=tmp      | B[0..7]           | ---> 缓存替换（额外的）
+-----------------------+-------------------+
|after B[2][1]=tmp      | B[0..7]           |
+-----------------------+-------------------+
|...                    |                   |
+-----------------------+-------------------+

额外的 miss 次数为 7 次（正常的形式: A[i][0], B[i][0], 额外的: B[1][1], B[2][2]...）
对角块上的总的 miss 次数是 16 + 7 = 23次.

  • 注意第17行，原始代码中after B[1][0]=tmp时tmp去需要去内存中读入A[0]，但由于tmp所对应的A[0][1]已经存放到CPU寄存器中，因此这里就不需要读取A[0]，自然也就不会驱逐B[0]。

  • 对于对角线上的分块，复制 A[m] 时会取代 B[m]( 第一行除外 )，将数据写入 B[m] 的时候又会重新加载一次。 所以，额外的 miss 次数为 7 次。对角块总的 miss 次数为 23 次。总的 miss 次数应该为 4×23+12×16=2844\times 23+12\times 16=284 次。

测试结果如下：

1
2
3
4
5
6
(cling) ➜  l4_cachelab ./test-trans -M 32 -N 32

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:1765, misses:288, evictions:256

实测的miss次数为288，和理论分析相差 4 次。

完美实现

前面提到的思路里 , 在对角线的分块处都无可避免的会产生 A, B 矩阵之间的缓存冲突。这个冲突真的不可避免吗？答案是否定的。实验要求上写了不能改变 A 矩阵，但是 B 可以随意处理。我们可以考虑在 B 矩阵上想点办法来消除两个矩阵之间的冲突。

为了消除对角线上分块行的相互替换，在实现中，每次先用局部变量缓存 A 分块的一行，再复制到 B 分块对应的行中。在复制完成后，B 的分块全部在缓存中，转置过程没有 miss。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int a0, a1, a2, a3, a4, a5, a6, a7;
for (int i = 0; i < 32; i += 8) {
    for (int j = 0; j < 32; j += 8) {
        // copy
        for (int k = i, s = j; k < i + 8; ++k, ++s) {
            a0 = A[k][j];
            a1 = A[k][j + 1];
            a2 = A[k][j + 2];
            a3 = A[k][j + 3];
            a4 = A[k][j + 4];
            a5 = A[k][j + 5];
            a6 = A[k][j + 6];
            a7 = A[k][j + 7];
            B[s][i] = a0;
            B[s][i+1] = a1;
            B[s][i+2] = a2;
            B[s][i+3] = a3;
            B[s][i+4] = a4;
            B[s][i+5] = a5;
            B[s][i+6] = a6;
            B[s][i+7] = a7;
        }
        // transpose
        for (int k = 0; k < 8; ++k)
            for (int s = k + 1; s < 8; ++s) {
                a0 = B[k + j][s + i];
                B[k + j][s + i] = B[s + j][k + i];
                B[s + j][k + i] = a0;
        }
    }
}

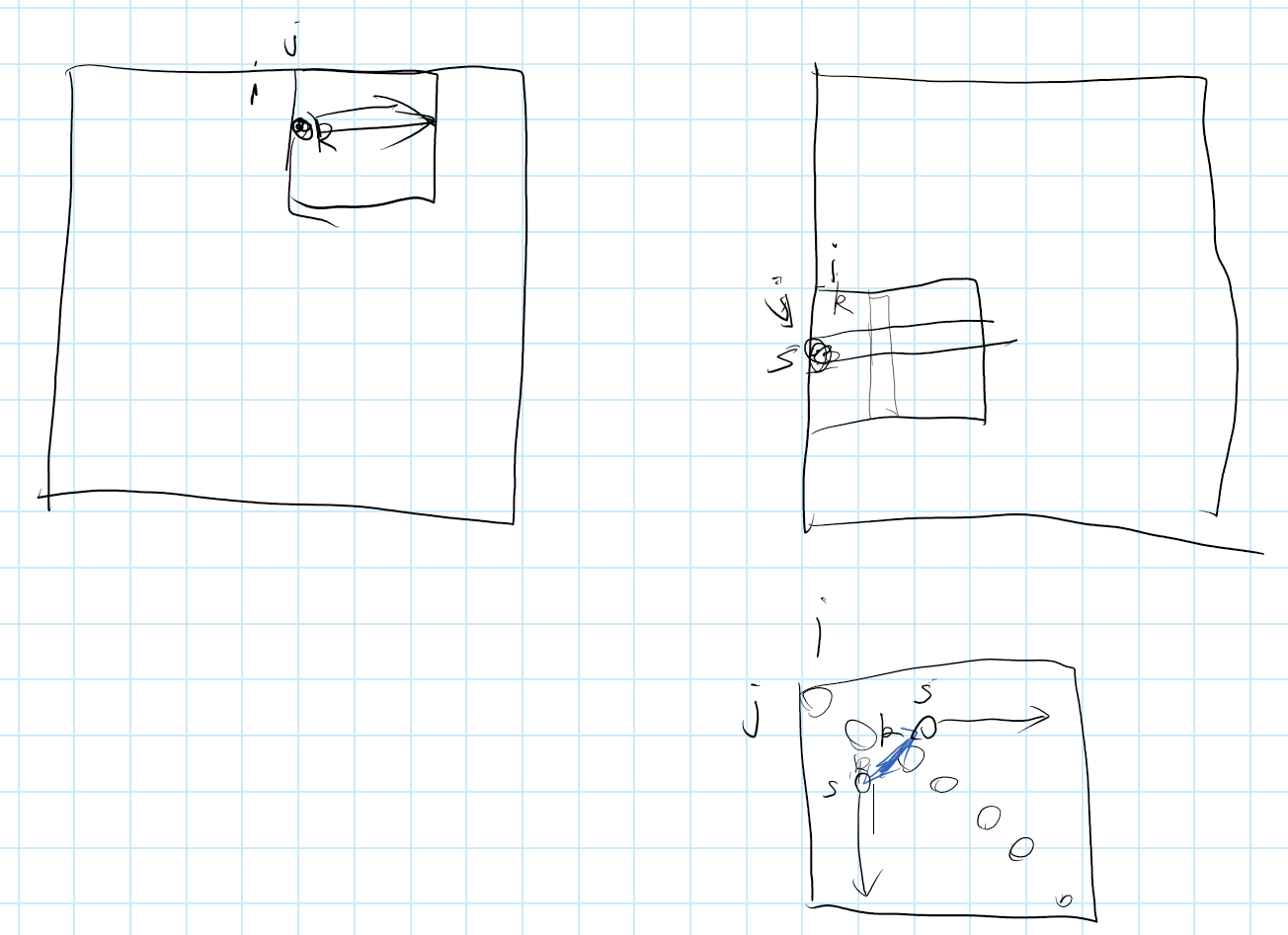
代码对应草稿图如下，编码时可以先画出草图，根据草图去写矩阵操作。

这个方法消除了所有的两个矩阵之间的缓存冲突，所以 miss 的理论次数是 16×16=25616\times 16=256。

实验测试：

1
2
3
4
5
6
(cling) ➜  l4_cachelab ./test-trans -M 32 -N 32

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:3585, misses:260, evictions:228

比理论分析多4次，这应该是能够达到的最好结果了。

64×64

每 4 行就会占满一个缓存，先考虑 4 × 4 分块，结果miss为1891次，没能拿到满分。

下面提供两种写法，二者来自“参考资料“一章中两篇不同的博客，二者本质一样，只是写法上一种使用一个缓冲区，另一种使用两个缓冲区，后者缓存不命中次数更少。

一个缓存区写法（简洁）

考虑 8 × 8 分块，由于存在着每 4 行就会占满一个缓存的问题，在分块内部处理时就需要技巧了，我们把分块内部分成 4 个 4 × 4 的小分块分别处理：

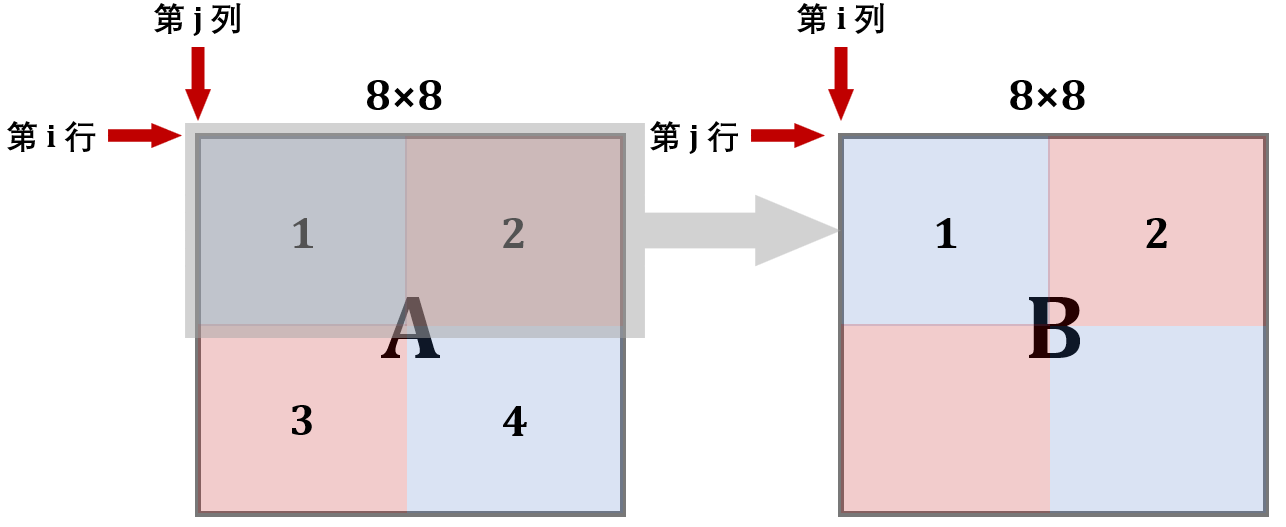
  • 第一步，将A的左上和右上一次性复制给B
  • 第二步，用本地变量把B的右上角存储下来
  • 第三步，将A的左下复制给B的右上
  • 第四步，利用上述存储B的右上角的本地变量，把A的右上复制给B的左下
  • 第五步，把A的右下复制给B的右下

画出图解如下：

这里的A和B均表示两个矩阵中的 8 × 8 块

第 1 步：

把 A 矩阵中1号和2号复制给 B 矩阵。

此时B的前 4 行就在缓存中了，接下来考虑利用这个缓存 。可以看到，为了利用A的缓存，第 2 块放置的位置实际上是错的，接下来就用本地变量保存B中 2 号块的内容。

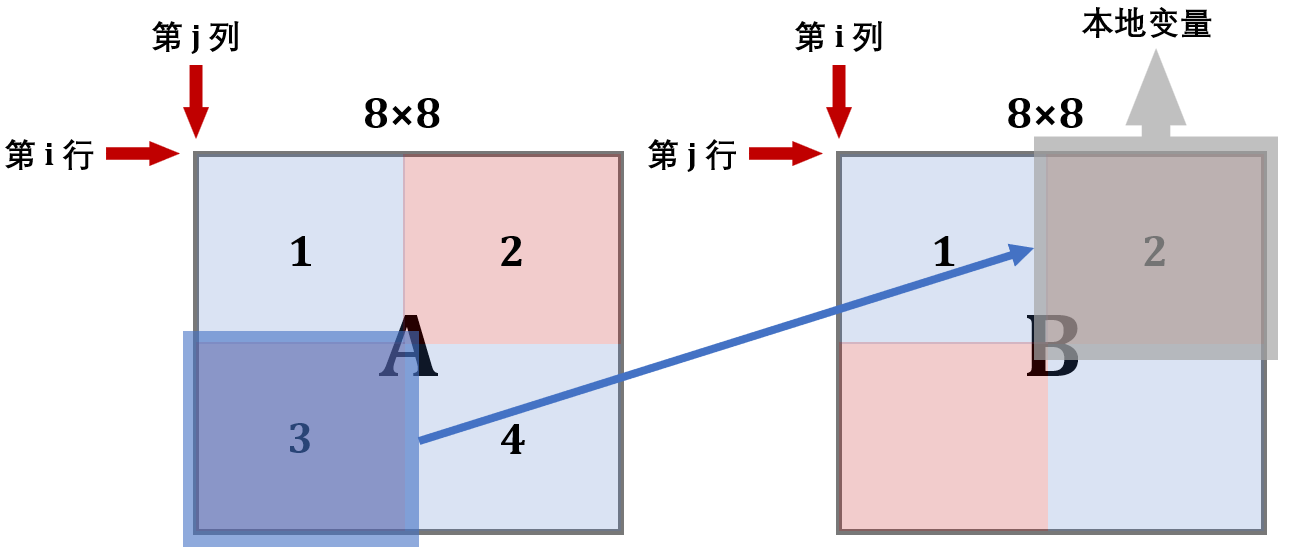
第 2 步：

用本地变量把B的 2 号块存储下来。

1
2
3
4
5
6
for (int k = j; k < j + 4; k++){
    a0 = B[k][i + 4];
    a1 = B[k][i + 5];
    a2 = B[k][i + 6];
    a3 = B[k][i + 7];
}

第 3 步：

现在缓存中还是存着B中上两块的内容，所以将A的 3 号块内容复制给它。

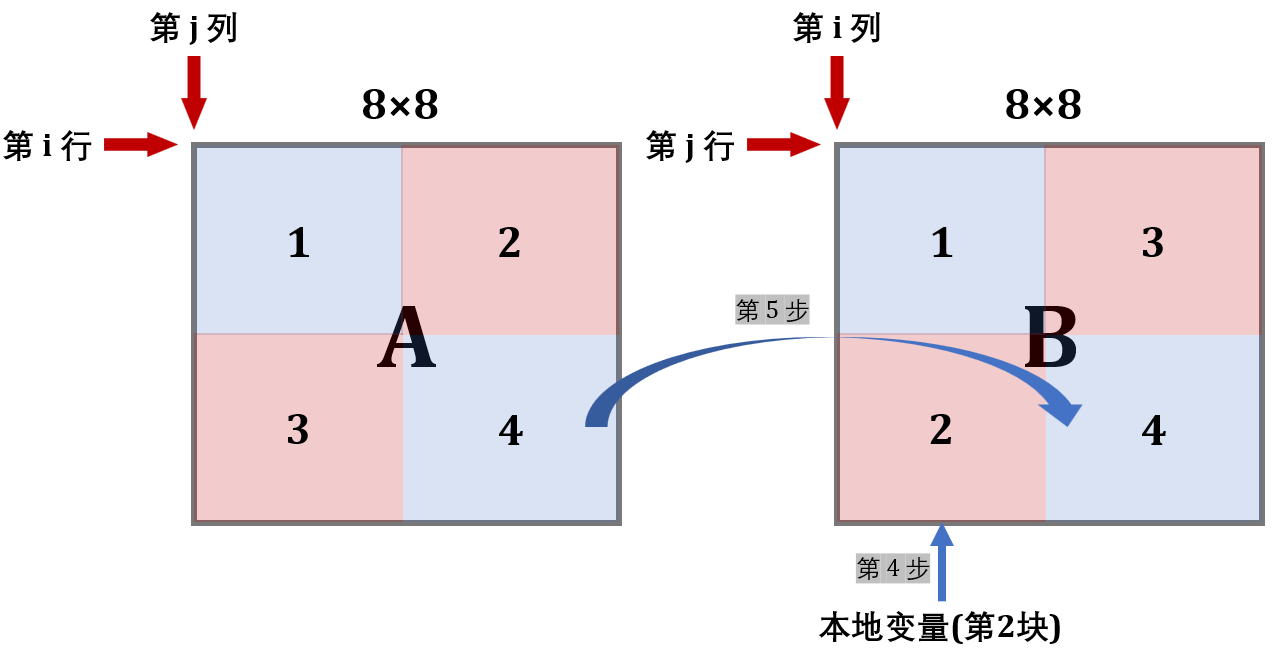
第 4/5 步：

现在缓存已经利用到极致了，可以开辟B的下面两块了。

这样就实现了转置，且消除了同一行中的冲突，具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
int a0, a1, a2, a3, a4, a5, a6, a7;
for (int i = 0; i < 64; i += 8){
    for (int j = 0; j < 64; j += 8){
        for (int k = i; k < i + 4; k++){
            // 得到A的第1,2块
            a0 = A[k][j + 0];
            a1 = A[k][j + 1];
            a2 = A[k][j + 2];
            a3 = A[k][j + 3];
            a4 = A[k][j + 4];
            a5 = A[k][j + 5];
            a6 = A[k][j + 6];
            a7 = A[k][j + 7];
            // 复制给B的第1,2块
            B[j + 0][k] = a0;
            B[j + 1][k] = a1;
            B[j + 2][k] = a2;
            B[j + 3][k] = a3;
            B[j + 0][k + 4] = a4;
            B[j + 1][k + 4] = a5;
            B[j + 2][k + 4] = a6;
            B[j + 3][k + 4] = a7;
        }
        for (int k = j; k < j + 4; k++){
            // 得到B的第2块
            a0 = B[k][i + 4];
            a1 = B[k][i + 5];
            a2 = B[k][i + 6];
            a3 = B[k][i + 7];
            // 得到A的第3块
            a4 = A[i + 4][k];
            a5 = A[i + 5][k];
            a6 = A[i + 6][k];
            a7 = A[i + 7][k];
            // 复制给B的第2块
            B[k][i + 4] = a4;
            B[k][i + 5] = a5;
            B[k][i + 6] = a6;
            B[k][i + 7] = a7;
            // B原来的第2块移动到第3块
            B[k + 4][i + 0] = a_0;
            B[k + 4][i + 1] = a_1;
            B[k + 4][i + 2] = a_2;
            B[k + 4][i + 3] = a_3;
        }
        for (int k = i + 4; k < i + 8; k++)
        {
            // 处理第4块
            a_4 = A[k][j + 4];
            a_5 = A[k][j + 5];
            a_6 = A[k][j + 6];
            a_7 = A[k][j + 7];
            B[j + 4][k] = a_4;
            B[j + 5][k] = a_5;
            B[j + 6][k] = a_6;
            B[j + 7][k] = a_7;
        }
    }
}

测试结果：

1
2
3
4
5
6
(cling) ➜  l4_cachelab ./test-trans -M 64 -N 64

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:9017, misses:1228, evictions:1196

两个缓冲区写法（高效）

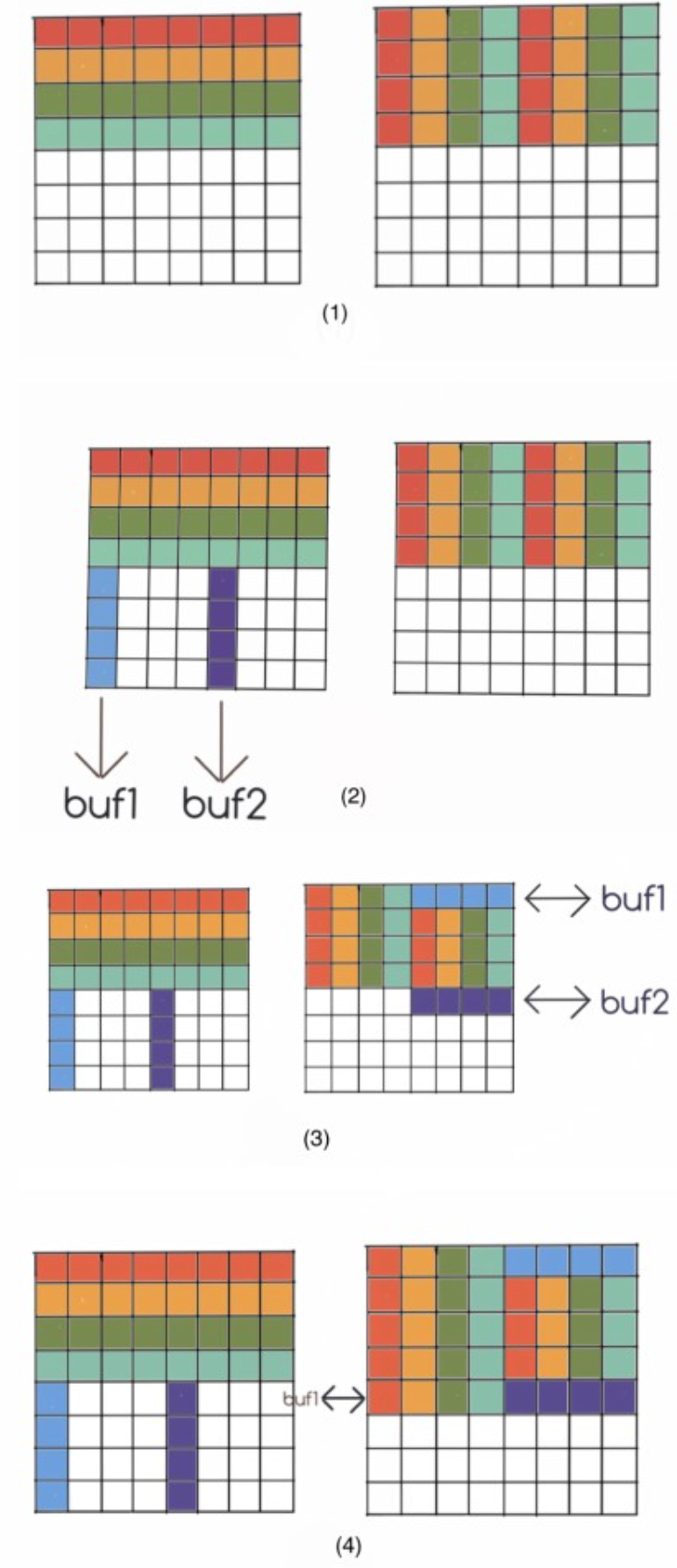
同样保持分块为 8 x 8，在大的分块下再分成 4 个 4 x 4 的小分块。我们先将 A 的前四行全部复制到 B 的前四行，这个时候 B 的左上角的元素在最终正确的位置，B 的右上角元素是应该放到左下角的元素。然后，我们在复制后 A 的后四行到 B 的过程中，利用本地变量将 B 右上角的内容复制到左下角。

具体步骤如下：

  1. 先将 A 的前四行按照 (1) 复制到 B 中。
  2. 按照 (2) 将 A 中对应位置的元素存到本地变量中。
  3. buf1 的四个元素与 B 右上角的第一行交换，将 buf2 中的值存到 B 右下角的对应位置。此时缓存中 B[4] 替换 B[0]。
  4. 将 buf1 中的元素存放到 B 左下角对应位置。
  5. 改变 8×8 块的位置，重复 (2)，(3)，(4)，直到所有元素到达正确位置。

可以看到，这种方法与上一种方法的本质上是完全一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
int block_size = 8;
for (int i = 0; i < N; i += block_size) {
    for (int j = 0; j < M; j += block_size) {
        for (int k = 0; k < block_size / 2; ++k) {
            // A top left
            a0 = A[k + i][j];
            a1 = A[k + i][j + 1];
            a2 = A[k + i][j + 2];
            a3 = A[k + i][j + 3];

            // copy
            // A top right
            a4 = A[k + i][j + 4];
            a5 = A[k + i][j + 5];
            a6 = A[k + i][j + 6];
            a7 = A[k + i][j + 7];

            // B top left
            B[j][k + i] = a0;
            B[j + 1][k + i] = a1;
            B[j + 2][k + i] = a2;
            B[j + 3][k + i] = a3;

            // copy
            // B top right
            B[j + 0][k + 4 + i] = a4;
            B[j + 1][k + 4 + i] = a5;
            B[j + 2][k + 4 + i] = a6;
            B[j + 3][k + 4 + i] = a7;
        }
        for (int k = 0; k < block_size / 2; k++) {
            // step 1 2
            a0 = A[i + 4][j + k], a4 = A[i + 4][j + k + 4];
            a1 = A[i + 5][j + k], a5 = A[i + 5][j + k + 4];
            a2 = A[i + 6][j + k], a6 = A[i + 6][j + k + 4];
            a3 = A[i + 7][j + k], a7 = A[i + 7][j + k + 4];
            // step 3
            tmp = B[j + k][i + 4], B[j + k][i + 4] = a0, a0 = tmp;
            tmp = B[j + k][i + 5], B[j + k][i + 5] = a1, a1 = tmp;
            tmp = B[j + k][i + 6], B[j + k][i + 6] = a2, a2 = tmp;
            tmp = B[j + k][i + 7], B[j + k][i + 7] = a3, a3 = tmp;
            // step 4
            B[j + k + 4][i + 0] = a0, B[j + k + 4][i + 4 + 0] = a4;
            B[j + k + 4][i + 1] = a1, B[j + k + 4][i + 4 + 1] = a5;
            B[j + k + 4][i + 2] = a2, B[j + k + 4][i + 4 + 2] = a6;
            B[j + k + 4][i + 3] = a3, B[j + k + 4][i + 4 + 3] = a7;
        }
    }
}

测试结果

1
2
3
4
5
6
(cling) ➜  l4_cachelab ./test-trans -M 64 -N 64

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:9137, misses:1108, evictions:1076

结果分析

这个实现会完全消除行同一个矩阵内部的冲突，但是两个矩阵之间的冲突没能完全避免。

对于在对角线上的块，步骤 (1) 会有 3 次额外 miss，步骤 (2)、(3)、(4)、(5) 有 7 次额外 miss。普通块 miss 次数仍然为 8。理论上总的 miss 次数为 (3+7)×8+64×8×2=1104(3+7)\times 8 + 64\times 8\times 2=1104。

步骤（1）中的三次 miss 可以通过先复制后转置的思路消除。

61×67

这个矩阵的转置要求很松，miss为 2000 以下就可以了。我也无心进行更深入的优化，直接 8 × 8 的分块就能通过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
for (int i = 0; i < N; i += 8) {
    for (int j = 0; j < M; j += 8) {
        if (i + 8 <= N && j + 8 <= M) {
            for (int s = j; s < j + 8; s++) {
                a0 = A[i][s];
                a1 = A[i + 1][s];
                a2 = A[i + 2][s];
                a3 = A[i + 3][s];
                a4 = A[i + 4][s];
                a5 = A[i + 5][s];
                a6 = A[i + 6][s];
                a7 = A[i + 7][s];
                B[s][i + 0] = a0;
                B[s][i + 1] = a1;
                B[s][i + 2] = a2;
                B[s][i + 3] = a3;
                B[s][i + 4] = a4;
                B[s][i + 5] = a5;
                B[s][i + 6] = a6;
                B[s][i + 7] = a7;
            }
        } else {
            for (int k = i; k < min(i + 8, N); k++) {
                for (int s = j; s < min(j + 8, M); s++) {
                    B[s][k] = A[k][s];
                }
            }
        }
    }
}

测试结果

1
2
3
4
5
6
(cling) ➜  l4_cachelab ./test-trans -M 61 -N 67

Function 0 (2 total)
Step 1: Validating and generating memory traces
Step 2: Evaluating performance (s=5, E=1, b=5)
func 0 (Transpose submission): hits:6315, misses:1864, evictions:1832

参考资料