Data Lab [Updated 12/16/19] (README, Writeup, Release Notes, Self-Study Handout)

Students implement simple logical, two’s complement, and floating point functions, but using a highly restricted subset of C. For example, they might be asked to compute the absolute value of a number using only bit-level operations and straightline code. This lab helps students understand the bit-level representations of C data types and the bit-level behavior of the operations on data.

实验作业网址：http://csapp.cs.cmu.edu/3e/labs.html

前言

本篇博客将会剖析 CSAPP - DataLab 各个习题的解题过程，加深对 int、unsigned、float 这几种数据类型的计算机表示方式的理解。

DataLab 中包含下表所示的 12 个习题，其中 9 个和整数有关，3个和单精度浮点数有关。

函数名 功能描述 分数 操作符
bitXor(x, y) 使用 & 和 ~ 实现异或操作 1 14
tmin() 补码的最小值 1 14
isTmax(x) x 是否为补码的最大值 1 10
allOddBits(x) x 的奇数位是否全为 1 2 12
negate(x) 不使用 - 计算 x 的相反数 2 5
isAsciDigit(x) x 是否在 [0x30, 0x39] 区间内 3 15
conditional 实现条件运算符，x ? y : z 3 16
isLessOrEqual(x, y) x 是否小于等于 y 3 24
logicalNeg(x) 不使用 ! 计算逻辑非 4 12
howManyBits(x) 表示 x 的最少补码位数 4 90
floatScale2(uf) 计算无符号数 uf 所表示的浮点数的 2 倍值 4 30
floatFloat2Int(uf) 将无符号数 uf 所表示的浮点数转为整数 4 30
floatPower2(x) 计算 2×2x2\times 2^x 4 30

bitXor

思路：先使用&、|、~进行表示，然后利用DeMorgan律去替换掉不能使用的位运算。

先画出真值表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
x y  x^y
0 0   0
0 1   1
1 0   1
1 1   0

x y  x|y
0 0   0
0 1   1
1 0   1
1 1   1

x y  x&y
0 0   0
0 1   0
1 0   0
1 1   1

思路1：看什么情况得到1

“x为0，y为1“或”x为1，y为0”即可：x^y = (x&~y) | (~x&y)

根据DeMorgan律：x|y = ~(~x & ~y)

即 x^y = (x&~y) | (~x&y) = ~(~(x&~y) & ~(~x&y))

思路2：排除掉得到0的情况

只要x、y不同时为0，或同时为1就行：x^y = ~(~x&~y) & ~(x&y)

思路3：^和|像，再用~(x&y)加掩码

x^y = x|y & ~(x&y)

利用DeMorgan律，得x^y = ~(~x&~y) & ~(x&y)

1
2
3
4
5
6
7
8
9
10
11
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
  // return ~(~(x&~y) & ~(~x&y));  // 思路1, 8次op
  return ~(x&y) & ~(~x&~y);  // 思路2和3，7次op
}

Tmin

Tmin形如1000000000，可通过移位表示：

1
2
3
4
5
6
7
8
9
10
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 0x80 << 24;  // 把高位的24位移掉
  // return 0x01 << 31;
}

isTmax

Tmax形如0111111…111，特点：~(Tmax+1)=Tmax，可通过这个性质判断

但是Umax = 1111111…111也满足 ~(Umax+1)=Umax，需要排除

二者不同在于Tmax+1不为0，而Umax+1等于0，”是否等于0“可以通过!!转化为布尔类型，否则直接&的话不对喔。

💡通过 !(x ^ y) 判断是否相等
通过 ! 或 !! 将结果转化为bool类型

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return !((~(x+1))^x) & !!(x+1);  // 8ops
}

addOddBits

首先产生1010…1010 即 0xAAAAAAAA 形式的掩码，对x的奇数位进行提取，然后判断提取结果是否为0xAAAAAAAA。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  int AA = 0xAA;
  int AAAA = AA << 8 | AA;
  int AAAAAAAA = AAAA << 16 | AAAA;
  return !((x & AAAAAAAA) ^ AAAAAAAA);  // 7ops
}

negate

💡 求负：逐位取反再加1

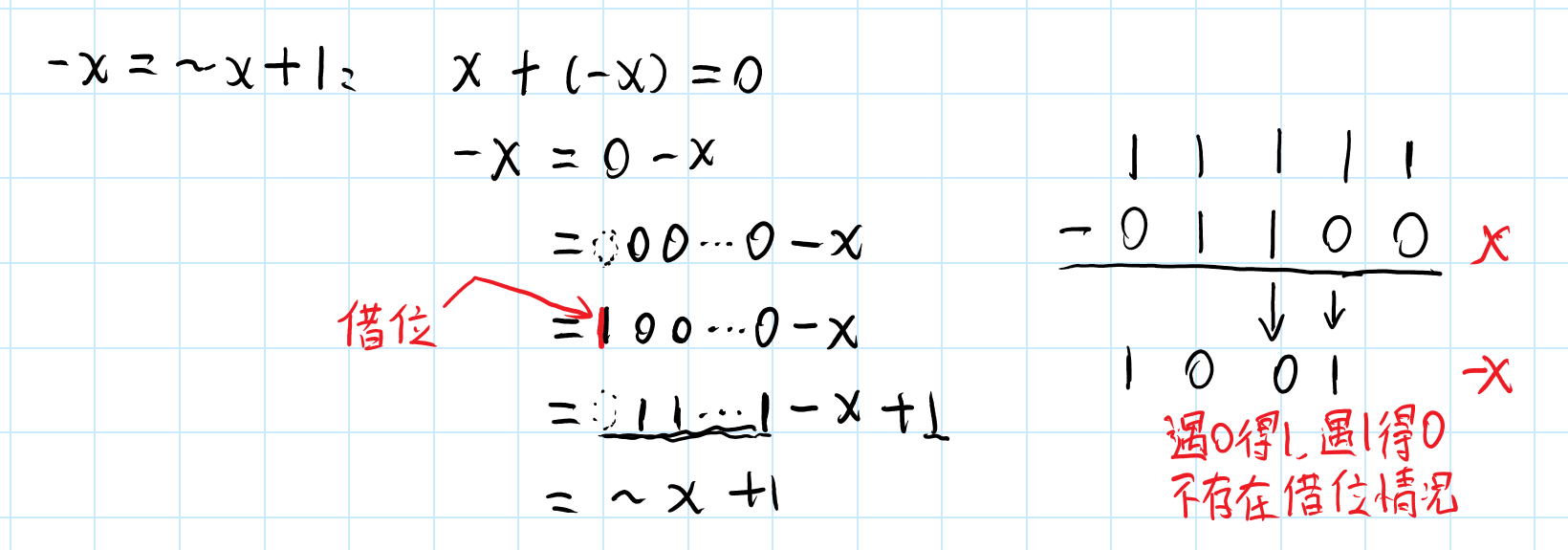
Untitled

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x + 1;
}

isAsciiDigit

0x30 位模式为 00…00 0011 0000

0x39 位模式为 00…00 0011 1001

可以分成两步来判断：

  1. 前24位为 00…00 0011
  2. 后8位范围为 0000-1001，判断方法为减去1010后，判断是否为负数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  int cond1 = !((x >> 4) ^ 0b11);
  int sub_res = (x & 0xF) + (~0xA + 1);  // 一定要加括号 &优先级比+/-低
  int cond2 = (sub_res >> 31) & 1;
  return cond1 & cond2;
}

conditional

结果一定形如：return (expr & y) | (~expr & z);

当x=0时，expr = 0, ~expr = 11…11

当x≠0时，expr = 11…11, ~exp = 0

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  // x =  0, mask = 00000000
  // x != 0, mask = 11111111
  int mask = !!(x) << 31 >> 31;
  return (mask & y) | (~mask & z);
}

isLessOrEqual

直接想法是做减法，判断差的符号。
但注意，只有同号时做+/-才不用考虑溢出，其他情况都需要单独判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
isLessOrEqual 等价于 x <= y ? 1 : 0;
然后去看什么样的情况下行

1 x == y
cond1 = !(x ^ y);

sign_x = (x >> 31) & 1
sign_y = (y >> 31) & 1
2 x + y -
cond2 = !(!sign_x & sign_y)  外层!表示x+ y-不行

3 x - y +
cond3 = sign_x & !sign_y

4 x - y - 此时做减法才不会溢出
int cond4 = (x + ~y + 1) >> 31 & 1

return cond1 | (cond2 & (cond3 | cond4))  不满足x+ y-并且...

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  int cond1 = !(x ^ y);
  int sign_x = x >> 31 & 1;
  int sign_y = y >> 31 & 1;
  int cond2 = !(~sign_x & sign_y);
  int cond3 = sign_x & ~sign_y;
  int cond4 = (x + ~y + 1) >> 31 & 1;
  return cond1 | (cond2 & (cond3 | cond4));
}

💡 优先级： ! ~ + << & |

logicalNeg

关键：找出0和非0数的关系，非0数有正负，x|(-x)的符号位一定为1

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  int neg_x = ~x + 1;
  int sign_x = (x | neg_x) >> 31;  // 0得到0，非0得到11..11
  return sign_x + 1;
}

howManyBits

  • 0 只需要1位表示
  • 负数，对于-1（111, 11111, 111111）都是只需要1位表示
    • 对于更一般的 1110 0011, 需要1位表示符号，然后将最高位0的位数命名位high_bit，则需要high_bit + 1位表示（可以通过取反，看最高位1确定high_bit）
      也可以这样理解：1位符号位+数值的无符号数表示，就像：bin(-7)='-0b111
  • 正数，需要1位符号位+数值表示

现在难点就变成如何求high_bit，即求最高位的1：

0010 0000 0000 0000 | 0000 0000 0000 0000
0000 0000 0000 0000 | 0001 0000 0000 0000

上面给出2个例子，首先看高16位是否有1

若有，右移动16位，继续去看1在哪（在高16位中同理去求）

若无，则意味着高16位全为0，不需要右移（在低16位中同理）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  int is_zero = !x;
  int is_neg = x >> 31;
  int mask = (!!x) << 31 >> 31;
  x = (is_neg & ~x) | (~is_neg & x);
  // 0010 0000 0000 0000 | 0000 0000 0000 0000
  // -------------------            16
  // 0000 0000 0000 0000 | 0001 0000 0000 0000
  //                       -------------------
  int bit_16 = !!(x >> 16) << 4;  // 16 0
  x >>= bit_16;
  int bit_8 = !!(x >> 8) << 3;
  x >>= bit_8;
  int bit_4 = !!(x >> 4) << 2;
  x >>= bit_4;
  int bit_2 = !!(x >> 2) << 1;
  x >>= bit_2;
  int bit_1 = !!(x >> 1);
  x >>= bit_1;
  int bit_0 = x;
  int high_bit = 1 + bit_16 + bit_8 + bit_4 + bit_2 + bit_1 + bit_0;
  return is_zero | (mask & high_bit);
}

floatScale2

F=(−1)s×M×2EF = (-1)^s\times M\times 2^{E}

  • 对于InF/NaN，直接输出argument
  • 对于非规范数，直接将frac左移1位——溢出到exp阶码域没关系，结果依然是对的
  • 对于规范数，由于E位于指数位置，E直接增一就行，exp = E + bias也是增一。由于EXP取值范围为[1, 254], 增加到255也没关系，INF/NaN都行。

💡对于Denormalized Values，frac直接左移1位，移除到阶码域结果也是正确的。
尾数域最高位权重为1/2， 移除到阶码域变成规范数后，M=1+frac，这时E由于解释方式的差异值不变，而M多的这个1恰好是1/2的2倍。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  int sign = uf >> 31;  // 无符号数使用逻辑右移
  int exp = (uf >> 23) & 0xFF;
  int frac = uf & 0x7FFFFF;

  if (exp == 0xFF) {  // Inf/NaN
    return uf;
  } else if (!exp) {  // denormalized number
    return sign << 31 | frac << 1;
  } else {  // normalized number
    ++exp;
    return sign << 31 | exp << 23 | frac;
  }
}

floatFloat2Int

先排除denormalized number和speical number，对于规范数：

先通过E = exp - 127 计算阶码

再通过 |0x800000 （5个0）把隐含的1加上，然后根据E进行移位

最后根据符号位，看是否需要加负号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  int sign = uf >> 31;
  int exp = uf >> 23 & 0xFF;
  int frac = uf & 0x7FFFFF;

  if (exp == 0xFF) {  // Inf/NaN
    return 0x80000000u;
  } else if (!exp) {  // denormalized number
    return 0;
  } else {
    int E = exp - 127;
    frac |= 0x800000;  // 后面有5个0: 20/4=5
    if (E >= 31) {
      return 0x80000000u;
    } else if (E >= 23) {
      frac <<= (E - 23);
    } else if (E >= 0) {
      frac >>= (23 - E);
    } else {
      return 0;
    }
    if (sign)  frac = ~frac + 1;
    return frac;
  }
}

floatPower2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
  //                        Min                    Max
  // denormalized: 2^(-23)*2^(1-127)=2^(-149)   <2^(-126)
  // normalized:   2^(-126)                     <2^(254-127)*2=2^(128)
  if (x < -149) {
    return 0;
  } else if (x < -126) {
		// denormalized
    // <--------------------------
    // ---> 负的越多，就需要往右退更多
    return (x + 127) << 23 | 1 << (23 + x + 126);
  } else if (x < 128) {
    return (x + 127) << 23;
  } else {
    return 0xFF << 23;
  }
}

参考资料