《剑指offer》笔记

AcWing版《剑指offer》的刷题笔记。

Week 1

找出数组中重复的数字★

给定一个长度为 $n$ 的整数数组 nums，数组中所有的数字都在 $0 \sim n - 1$ 的范围内。

数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。

请找出数组中任意一个重复的数字。

注意：如果某些数字不在 $0 \sim n - 1$ 的范围内，或数组中不包含重复数字，则返回 -1；

数据范围

$0 \le n \le 1000$

样例

给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。

返回 2 或 3。

原地哈希

时间复杂度： $O(n)$

思路

nums[i] 的值为 nums[i], 而 nums[nums[i]] 元素的下标位置为 nums[i],
每次swap后nums[i]被放到下标为nums[i]的位置处(而i处的值nums[i]会变化)，因此不会死循环, while可以结束

while结束的条件是: nums[i] == nums[nums[i]], 这有2种情况:

1. i == nums[i], 即成功把i处元素也放好
2. i != nums[i], 即下标为i和nums[i]的值相等nums[i] == nums[nums[i]], 碰撞发生, 返回

时空复杂度分析

• 时间复杂度: $O(n)$, 每次swap都会有1个元素放回原位
• 空间复杂度: $O(1)$, 没有开辟新数组

class Solution {
public:
  int duplicateInArray(vector<int>& nums) {
    int n = nums.size();
    for (auto x: nums) {
      if (x < 0 || x > n - 1) return -1;
    }
    for (int i = 0; i < n; i++) {
      while (nums[i] != nums[nums[i]]) swap(nums[i], nums[nums[i]]);
      if (i != nums[i]) return nums[i];
    }
    return -1;
  }
};

这道题在原书上绝对不是简单级别啊！
它考察的是程序员的沟通能力，先问面试官要时间/空间需求！！！
只是时间优先就用字典，
还有空间要求，就用指针+原地排序数组，
如果面试官要求空间O(1)并且不能修改原数组，还得写成二分法！！！

不修改数组找出重复的数字★

给定一个长度为 $n + 1$ 的数组nums，数组中所有的数均在 $1 \sim n$ 的范围内，其中 $n \ge 1$。

请找出数组中任意一个重复的数，但不能修改输入的数组。

数据范围

$1 \le n \le 1000$

样例

给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。

返回 2 或 3。

思考题：如果只能使用 $O(1)$ 的额外空间，该怎么做呢？

抽屉原理 + 二分法

时复度： $O(n\cdot logn)$

抽屉原理: n+1个数的取值范围为[1, n], 则必有至少2个数相同

分治思想: 将取值范围总区间[1, n]按取值范围分为左右区间, 则必有1个区间中的数大于坑数(取值范围个数)。

每次会将区间长度缩小一半，一共会缩小 $O(logn)$ 次。每次统计两个子区间中的数时需要遍历整个数组，时间复杂度是 $O(n)$。所以总时间复杂度是 $O(nlogn)$。

class Solution {
public:
  int duplicateInArray(vector<int>& nums) {
    // 二分的是取值范围(坑的范围)
    int l = 1, r = nums.size() - 1;  // nums.size() = n + 1
    while (l < r) {
      int mid = (l + r) >> 1;
      int s = 0;
      for (auto x: nums) s += (x >= l && x <= mid);
      if (s > mid - l + 1) r = mid;
      else l = mid + 1;
    }
    return l;
  }
};

二维数组中的查找

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。

请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

数据范围

二维数组中元素个数范围 $[0,1000]$

样例

输入数组：

[
  [1,2,8,9]，
  [2,4,9,12]，
  [4,7,10,13]，
  [6,8,11,15]
]

如果输入查找数值为7，则返回true，

如果输入查找数值为5，则返回false。

Binary Search Tree 单调性扫描 $O(n + m)$

寻找突破点时可以关注边界, 此题的突破点在右上角
右上角同行向左的元素都比其小, 同列向下的所有元素均比其大
当右上角元素比target大时, 所在列都不用考虑(j–),比target小时所在行都不用考虑(i++)

class Solution {
public:
  bool searchArray(vector<vector<int>> array, int target) {
    if (array.empty()) return false;
    int n = array.size(), m = array[0].size();
    int i = 0, j = m - 1;
    while (i < n && j >= 0) {
      if (array[i][j] == target) return true;
      else if (array[i][j] > target) j--;
      else i++;
    }
    return false;
  }
};

替换空格

请实现一个函数，把字符串中的每个空格替换成"%20"。

数据范围

$0 \le$ 输入字符串的长度 $\le 1000$。
注意输出字符串的长度可能大于 $1000$。

样例

输入："We are happy."

输出："We%20are%20happy."

遍历添加 $O(n)$

class Solution {
public:
  string replaceSpaces(string &str) {
    string res;
    for (auto x: str) {
      if (x == ' ') {
        res += "%20";
      } else { 
        res += x;
      }
    }
    return res;
  }
};

本地修改

Python / Java 中字符串被设计成不可修改的，而在 C++ 中字符串是可变的。

class Solution {
public:
  string replaceSpace(string s) {
    int count = 0, len = s.size();
    for (int i = 0; i < len; i++) {
      if (s[i] == ' ') count++;
    }
    s.resize(len + 2 * count);
    for (int i = len - 1, j = s.size() - 1; i < j; i--, j--) {
      if (s[i] != ' ') {
        s[j] = s[i];
      } else {
        s[j - 2] = '%';
        s[j - 1] = '2';
        s[j] = '0';
        j -= 2;
      }
    }
    return s;
  }
};

从尾到头打印链表

输入一个链表的头结点，按照 从尾到头 的顺序返回节点的值。

返回的结果用数组存储。

数据范围

$0 \le$ 链表长度 $\le 1000$。

样例

输入：[2, 3, 5]
返回：[5, 3, 2]

解法1 翻转vector

时复：$O(n)$

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  vector<int> printListReversingly(ListNode* head) {
    vector<int> res;
    while (head) {
      res.push_back(head->val);
      head = head->next;
    }
    reverse(res.begin(), res.end());
    return res;
  }
};

reverse() 原理是通过交换容器中元素的位置，将首尾元素、次首次尾元素等逐个交换，从而实现整个容器的反转

解法2 辅助栈

时复：$O(n)$

class Solution {
public:
  vector<int> printListReversingly(ListNode* head) {
    stack<int> stk;
    while (head) {
      stk.push(head->val);
      head = head->next;
    }
    vector<int> res;
    while (stk.size()) {
      res.push_back(stk.top());
      stk.pop();
    }
    return res;
  }
};

重建二叉树

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

注意:

• 二叉树中每个节点的值都互不相同；
• 输入的前序遍历和中序遍历一定合法；

数据范围

树中节点数量范围 $[0,100]$。

样例

给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]

返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示：
    3
   / \
  9  20
    /  \
   15   7

题解

思路

先序遍历第1个对应的为根节点, 在中序遍历序列中找到其位置为k, 那么[il, k-1]为左子树的中序序列, 而[k+1, ir]为右子数的中序序列
根据区间长度可以确定先序遍历序列中左子树的端点, 从而递归去求解。

时间复杂度

在初始化时，用哈希表记录每个值在中序遍历序列中的位置，这样我们在递归到每个节点时，在中序遍历中查找根节点位置的操作，只需要 $O(1)$ 的时间。此时，创建每个节点需要的时间是 $O(1)$，所以总时间复杂度是 $O(n)$。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  vector<int> pre, in;
  map<int, int> pos;
  TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
    pre = _preorder, in = _inorder;
    for (int i = 0; i < pre.size(); i++) pos[in[i]] = i;
    return dfs(0, pre.size() - 1, 0, in.size() - 1);
  }
  
  // 返回区间先序和中序遍历序列对应的子树的根
  TreeNode* dfs(int pl, int pr, int il, int ir) {
    if (pl > pr) return nullptr;
    TreeNode *root = new TreeNode(pre[pl]);
    int k = pos[pre[pl]];
    root->left = dfs(pl + 1, pl + k - il, il, k - 1);
    root->right = dfs(pl + k - il + 1, pr, k + 1, ir);
    return root;
  }
};

二叉树的下一个节点★

给定一棵二叉树的其中一个节点，请找出中序遍历序列的下一个节点。

注意：

• 如果给定的节点是中序遍历序列的最后一个，则返回空节点;
• 二叉树一定不为空，且给定的节点一定不是空节点；

数据范围

树中节点数量 $[0,100]$。

样例

假定二叉树是：[2, 1, 3, null, null, null, null]， 给出的是值等于2的节点。

则应返回值等于3的节点。

解释：该二叉树的结构如下，2的后继节点是3。
  2
 / \
1   3

题解

思路

二叉树的中序遍历：{ [左子树], 根节点, [右子树] }

• 情况1. 存在右儿子, 则为右子树的最左端
• 情况2. 不存在右儿子, 则需要沿着father域一直向上找，找到第1个是其father左儿子的节点，该节点的father就是当前节点的后继。即一直向左上找, 直到出现拐点(向右上), 那么拐点则为目标点(可从拐点角度再去理解)

时间复杂度
不论往上找还是往下找，总共遍历的节点数都不大于树的高度。所以时间复杂度是 $O(h)$，其中 $h$ 是树的高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode *father;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}
 * };
 */
class Solution {
public:
  TreeNode* inorderSuccessor(TreeNode* p) {
    if (p->right) {
      p = p->right;
      while (p->left) p = p->left;
      return p;
    }
    while (p->father && p == p->father->right) p = p->father;
    return p->father;
  }
};	

用两个栈实现队列

请用栈实现一个队列，支持如下四种操作：

• push(x) – 将元素x插到队尾；
• pop() – 将队首的元素弹出，并返回该元素；
• peek() – 返回队首元素；
• empty() – 返回队列是否为空；

注意：

• 你只能使用栈的标准操作：push to top，peek / pop from top, size 和 is empty；
• 如果你选择的编程语言没有栈的标准库，你可以使用list或者deque等模拟栈的操作；
• 输入数据保证合法，例如，在队列为空时，不会进行pop或者peek等操作；

数据范围

每组数据操作命令数量 $[0,100]$。

样例

MyQueue queue = new MyQueue();

queue.push(1);
queue.push(2);
queue.peek();  // returns 1
queue.pop();   // returns 1
queue.empty(); // returns false

解法

栈是“先进后出，后进先出”，两句话联系在一起很自然可以得出：两个栈可以实现“先进先出”。

class MyQueue {
public:
  stack<int> stk, cache;
  void copy(stack<int> &source, stack<int> &dest) {  // &, 否则报Segmentation Fault
    while (source.size()) {
      dest.push(source.top());
      source.pop();
    }
  }
  
  /** Initialize your data structure here. */
  MyQueue() {
      
  }
  
  /** Push element x to the back of queue. */
  void push(int x) {
    stk.push(x);  
  }
  
  /** Removes the element from in front of queue and returns that element. */
  int pop() {
    copy(stk, cache);
    int res = cache.top();
    cache.pop();
    copy(cache, stk);
    return res;
  }
  
  /** Get the front element. */
  int peek() {
    copy(stk, cache);
    int res = cache.top();
    copy(cache, stk);
    return res;
  }
  
  /** Returns whether the queue is empty. */
  bool empty() {
    return stk.empty();
  }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * bool param_4 = obj.empty();
 */

斐波那契数列

输入一个整数 $n$ ，求斐波那契数列的第 $n$ 项。

假定从 $0$ 开始，第 $0$ 项为 $0$。

数据范围

$0 \le n \le 39$

样例

输入整数 n=5 

返回 5

题解 $O(n)$

class Solution {
public:
  int Fibonacci(int n) {
    int a = 0, b = 1;
    while (n -- ) {
      int c = a + b;
      a = b, b = c;
    }
    return a;
  }
};

旋转数组的最小数字★

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

输入一个升序的数组的一个旋转，输出旋转数组的最小元素。

例如数组 $\{3,4,5,1,2\}$ 为 $\{1,2,3,4,5\}$ 的一个旋转，该数组的最小值为 $1$。

数组可能包含重复项。

注意：数组内所含元素非负，若数组大小为 $0$，请返回 $-1$。

数据范围

数组长度 $[0,90]$。

样例

输入：nums = [2, 2, 2, 0, 1]

输出：0

预处理 + 二分

思路

二分本质: 一半区间满足某种性质, 而另一半区间全部不满足, 这题不能直接使用二分。
由于重复元素的存在, 左边所有元素都>=nums[0], 而右边并非所有元素都不满足(并不全严格<nums[0)：末尾重复元素满足>=nums[0]
去掉右重后, 左边严格>=nums[0], 右边严格<nums[0], 可用二分。

时间复杂度
二分的时间复杂度是 $O(logn)$，删除最后水平一段的时间复杂度最坏是 $O(n)$，所以总时间复杂度是 $O(n)$。

class Solution {
public:
  int findMin(vector<int>& nums) {
    if (nums.empty()) return -1;
    int r = nums.size() - 1;
    while (r > 0 && nums[r] == nums[0]) r--;
    if (nums[r] > nums[0]) return nums[0];  // 判断是否单调
    int l = 0;
    while (l < r) {
      int mid = (l + r) >> 1;
      if (nums[mid] < nums[0]) {  // <nums[0]，而非nums[mid]
        r = mid;
      } else {
        l = mid + 1;
      }
    }
    return nums[l];
  }
};

矩阵中的路径★

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。

路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。

如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。

注意：

• 输入的路径不为空；
• 所有出现的字符均为大写英文字母；

数据范围

矩阵中元素的总个数 $[0,900]$。
路径字符串的总长度 $[0,900]$。

样例

matrix=
[
  ["A","B","C","E"],
  ["S","F","C","S"],
  ["A","D","E","E"]
]

str="BCCE" , return "true" 

str="ASAE" , return "false"

DFS大法好

经典的DFS

自己多练练，这么简单的题目一定要写对啦！

时间复杂度分析

单词起点一共有 $n^2$ 个，单词的每个字母一共有上下左右四个方向可以选择，但由于不能走回头路，所以除了单词首字母外，仅有三种选择。所以总时间复杂度是 $O(n^23^k)$

class Solution {
public:
  vector<vector<char>> mat;
  string str;
  int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
  
  bool hasPath(vector<vector<char>> &_matrix, string &_str) {
    mat = _matrix, str = _str;
    for (int i = 0; i < mat.size(); i++) {
      for (int j = 0; j < mat[0].size(); j++) {
        if (dfs(i, j, 0)) return true;
      }
    }
    return false;
  }
  
  bool dfs(int x, int y, int d) {  // 形参不要用i,j, 因为循环常用
    if (mat[x][y] != str[d]) return false;
    if (d == str.size() - 1) return true;
    
    char t = mat[x][y];  // 将匹配过的字符改为特殊字符, 防止重复匹配
    mat[x][y] = '@';
    for (int i = 0; i < 4; i++) {
      int a = x + dx[i], b = y + dy[i];
      if (a >= 0 && a < mat.size() && b >= 0 && b < mat[0].size()) {
        if (dfs(a, b, d + 1)) return true;
      }
    }
    mat[x][y] = t;  // u+1在3个方向(4个除去来时位置)都无法匹配, u处往后无法匹配, 放弃时需要回溯
    return false;
  }
};

---

Week 2

机器人的运动范围★

地上有一个 $m$ 行和 $n$ 列的方格，横纵坐标范围分别是 $0 \sim m - 1$ 和 $0 \sim n - 1$。

一个机器人从坐标 $(0,0)$ 的格子开始移动，每一次只能向左，右，上，下四个方向移动一格。

但是不能进入行坐标和列坐标的数位之和大于 $k$ 的格子。

请问该机器人能够达到多少个格子？

注意:

1. 0<=m<=50
2. 0<=n<=50
3. 0<=k<=100

样例1

输入：k=7, m=4, n=5

输出：20

样例2

输入：k=18, m=40, n=40

输出：1484

解释：当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。
      但是，它不能进入方格（35,38），因为3+5+3+8 = 19。

BFS大法好 $O(nm)$

注意题目要求“每一次只能向左，右，上，下四个方向移动一格”，所以使dfs或者bfs就能不重不漏的求得结果，。

一定要能熟练写对呀。

class Solution {
public:
  int get_sum(int x, int y) {
    int sum = 0;
    while (x) {
      sum += x % 10;
      x /= 10;
    }
    while (y) {
      sum += y % 10;
      y /= 10;
    }
    return sum;
  }

  int movingCount(int threshold, int rows, int cols) {
    if (!rows || !cols) return 0;
    
    int res = 0;
    vector<vector<bool>> st(rows, vector<bool>(cols, false));
    queue<pair<int, int>> q;
    q.push({0, 0});
    
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    while (q.size()) {
      auto t = q.front();
      q.pop();
      
      int x = t.first, y = t.second;
      if (st[x][y] || get_sum(x, y) > threshold) continue;
      st[x][y] = true;
      res++;
      
      for (int i = 0; i < 4; i++) {
        int a = x + dx[i], b = y + dy[i];
        if (a >= 0 && a < rows && b >= 0 && b < cols && !st[a][b]) {
          q.push({a, b});
        }
      }
    }
    return res;
  }
};

错误写法

“判断是否走过”一定要放到res++前，下面这样写会导致算结果偏多：

3	4
1	2

1号出队列后会将2和3入队，3出队列时会将4入队，此时2比4更靠近队头，所以2出对时会将4重复入队。
虽然在入队后，马上标记st[a][b] = true就能解决问题，但是还是更推荐上面的思路和写法。

int movingCount(int threshold, int rows, int cols) {
  if (!rows || !cols) return 0;
    
  int res = 0;
  vector<vector<bool>> st(rows, vector<bool>(cols, false));
  queue<pair<int, int>> q;
  q.push({0, 0});
    
  int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
  while (q.size()) {
    auto t = q.front();
    q.pop();
    int x = t.first, y = t.second;
    st[x][y] = true;
    if (get_sum(x, y) > threshold) continue;
    res++;
    for (int i = 0; i < 4; i++) {
      int a = x + dx[i], b = y + dy[i];
      if (a >= 0 && a < rows && b >= 0 && b < cols && !st[a][b]) {
        q.push({a, b});
      }
    }
  }
  return res;

剪绳子

给你一根长度为 $n$ 绳子，请把绳子剪成 $m$ 段（$m$、$n$ 都是整数，$2 \le n \le 58$ 并且 $m \ge 2$）。

每段的绳子的长度记为 $k[1]、k[2]、……、k[m]$。

$k[1]k[2] … k[m]$ 可能的最大乘积是多少？

例如当绳子的长度是 $8$ 时，我们把它剪成长度分别为 $2、3、3$ 的三段，此时得到最大的乘积 $18$。

样例

输入：8

输出：18

数学分析 $O(n)$

以下分析来自于y总
本人建议按数字大小从2到5、6分析就能发现规律了（做过此题的前提下）

这道题目是数学中一个很经典的问题。
下面我们给出证明：

首先把一个正整数 $N$ 拆分成若干正整数只有有限种拆法，所以存在最大乘积。
假设 $N=n_1+n_2+\cdots +n_k$，并且 $n_1×n_2×\cdots ×n_k$ 是最大乘积。

1. 显然1不会出现在其中；
2. 如果对于某个 $i$ 有 $n_i\ge 5$那么把 $n_i$ 拆分成 $3+(n_i−3)$，我们有 $3(n_i−3)=3n_i−9>n_i$；
3. 如果 $n_i=4$，拆成 $2+2$乘积不变，所以不妨假设没有4；
4. 如果有3个以上的2，那么 $3×3>2×2×2$，所以替换成3乘积更大；

综上，选用尽量多的3，直到剩下2或者4时，用2。

时间复杂度分析：当 n 比较大时，n 会被拆分成 ⌈n/3⌉ 个数，我们需要计算这么多次减法和乘法，所以时间复杂度是 $O(n)$。

class Solution {
public:
  int integerBreak(int n) {
    if (n <= 3) return 1 * (n - 1);
    int res = 1;
    if (n % 3 == 1) res = 4, n -= 4;
    else if (n % 3 == 2) res = 2, n -= 2;
    while (n) res *= 3, n -= 3;
    return res;
  }
};

二进制中1的个数

输入一个 $32$ 位整数，输出该数二进制表示中 $1$ 的个数。

注意：

• 负数在计算机中用其绝对值的补码来表示。

数据范围

$-100 \le$ 输入整数 $\le 100$

样例1

输入：9
输出：2
解释：9的二进制表示是1001，一共有2个1。

样例2

输入：-2
输出：31
解释：-2在计算机里会被表示成11111111111111111111111111111110，
      一共有31个1。

法1 转化为unsigned避免移位补符号数 $O(logn)$

需要转化为unsigned, 否则>>时会在左边填充符号位1。

class Solution {
public:
  int NumberOf1(int n) {
    unsigned int un = n;
    int res = 0;
    while (un) {
      res += un & 1;
      un >>= 1;
    }
    return res;
  }
};

法2 使用lowbit()函数 $O(logn)$

不用转化为unsigned, 即 $lowbit(x) = x \& -x, \forall x \in Z$。

class Solution {
public:
  int NumberOf1(int n) {
    int res = 0;
    while (n) {
      n = n - (n & -n);
      res++;
    }
    return res;
  }
};

数值的整数次方★

实现函数_double Power(double base, int exponent)_，求_base_的 _exponent_次方。

不得使用库函数，同时不需要考虑大数问题。

只要输出结果与答案的绝对误差不超过 $10^{-2}$ 即视为正确。

注意：

• 不会出现底数和指数同为0的情况
• 当底数为0时，指数一定为正
• 底数的绝对值不超过 $10$，指数的绝对值不超过 $10^9$。

样例1

输入：10 ，2

输出：100

样例2

输入：10 ，-2  

输出：0.01

经典快速幂算法 $O(logn)$

需要转化为long long的原因: int的取值范围为$[-2^{31}, 2^{31}-1)$, 而abs(-2^31)会溢出

class Solution {
public:
  double Power(double base, int exponent) {
    typedef long long LL;
    double res = 1;
    for (LL k = abs(LL(exponent)); k; k >>= 1) {
      if (k & 1) res *= base;
      base *= base;
    }
    if (exponent < 0) res = 1 / res;
    return res;
  }
};

在O(1)时间删除链表结点

给定单向链表的一个节点指针，定义一个函数在$O(1)$时间删除该结点。

假设链表一定存在，并且该节点一定不是尾节点。

数据范围

链表长度 $[1,500]$。

样例

输入：链表 1->4->6->8
      删掉节点：第2个节点即6（头节点为第0个节点）

输出：新链表 1->4->8

替身

由于是单链表，我们不能找到前驱节点，所以我们不能按常规方法将该节点删除。
我们可以换一种思路，将下一个节点的值复制到当前节点，然后将下一个节点删除即可。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        auto p = node->next;  // 将下一节点的val和next赋值给本节点, 再删除下一节点
        node->val = p->val;
        node->next = p->next;
        delete p;  // 防止内存泄露
    }
};
```

删除链表中重复的节点★

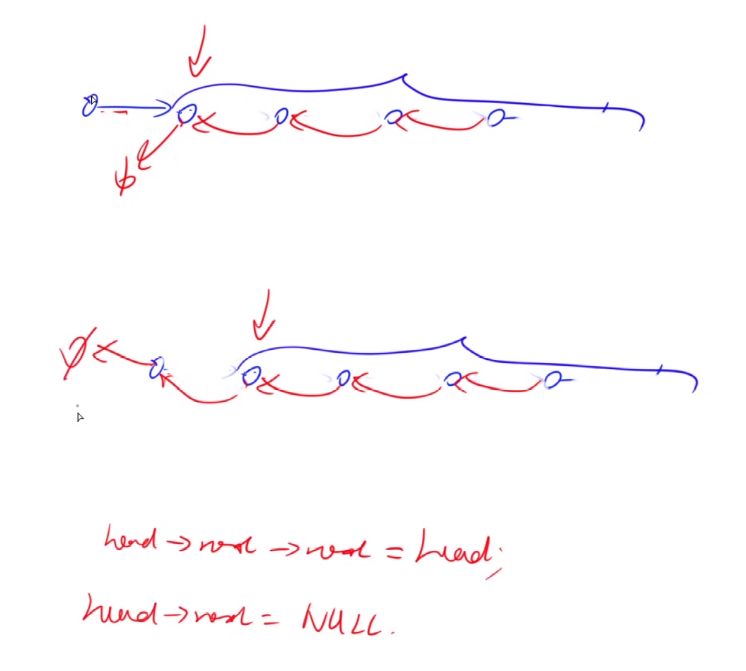
在一个排序的链表中，存在重复的节点，请删除该链表中重复的节点，重复的节点不保留。

数据范围

链表中节点 val 值取值范围 $[0,100]$。
链表长度 $[0,100]$。

样例1

输入：1->2->3->3->4->4->5

输出：1->2->5

样例2

输入：1->1->1->2->3

输出：2->3

题解

把排序好的链表看成一段段的, 有长度为1的段, 也有长度>=2的重复元素组成的段。
从前往后扫描整个链表，每次扫描元素相同的一段，如果这段中的元素个数多于1个，则将整段元素直接删除。

时复：$O(n)$

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplication(ListNode* head) {
        auto dummy = new ListNode(-1);  // 凡是可能删除head的情况, 都应加个不会被删除的dummy节点
        dummy->next = head;
        auto p = dummy;  // p指向上一个长度为1的段的为指针
        while (p->next) {
            auto q = p->next;
            while (q && p->next->val == q->val) q = q->next;
            if (p->next->next == q) p = p->next;
            else p->next = q;
        }
        return dummy->next;
    }
};

正则表达式匹配🤯

请实现一个函数用来匹配包括'.'和'*'的正则表达式。

模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。

在本题中，匹配是指字符串的所有字符匹配整个模式。

例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但是与"aa.a"和"ab*a"均不匹配。

数据范围

输入字符串长度 $[0,300]$。

样例

输入：

s="aa"
p="a*"

输出:true

DP大法好 $O(nm)$

状态表示 f[i][j]表示s[i,...]与p[j,...]是否相匹配

状态计算

1. p[j]是正常字符, f[i][j] = (s[i] == p[j] && f[i+1][j+1])

2. p[j] = ‘.’, f[i][j] = f[i+1][j+1]

3. p[j+1] = ‘*’, f[i][j] = f[i][j+2] || (s[i] == p[j] && f[i+1][j])

   f[i][j+2]对应 '*'表示0个p[j]
   s[i]==p[j] && f[i+1][j] 对应 非0任意多个p[j] 这里是最难的

边界情况 f[n][m] = true

时间复杂度分析

$n$ 表示s的长度，$m$ 表示p的长度，总共 $nm$ 个状态，状态转移复杂度 $O(1)$，所以总时间复杂度是 $O(nm)$.

class Solution {
public:
  string s, p;
  int n, m;
  vector<vector<int>> f;
  
  bool isMatch(string _s, string _p) {
    s = _s, p = _p;
    n = s.size(), m = p.size();
    // vector<vector<int>> f(n + 1, vector<int>(m + 1, -1));  // 错误写法
    f = vector<vector<int>>(n + 1, vector<int>(m + 1, -1));  // n + 1, 而非n
    return dp(0, 0);
  }
  
  bool dp(int x, int y) {
    if (f[x][y] != -1) return f[x][y];
    if (y == m) {  // x对应n, y对应m
      return f[x][y] = x == n;
    }
    bool first_match = x < n && (p[y] == '.' || s[x] == p[y]);
    if (y + 1 < m && p[y + 1] == '*') {
      f[x][y] = dp(x, y + 2) || (first_match && dp(x + 1, y));
    } else {
      f[x][y] = first_match && dp(x + 1, y + 1);
    }
    return f[x][y];
  }
};

表示数值的字符串🤯

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

例如，字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。

但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。

注意:

1. 小数可以没有整数部分，例如.123等于0.123；
2. 小数点后面可以没有数字，例如233.等于233.0；
3. 小数点前面和后面可以有数字，例如233.666;
4. 当e或E前面没有数字时，整个字符串不能表示数字，例如.e1、e1；
5. 当e或E后面没有整数时，整个字符串不能表示数字，例如12e、12e+5.4;

数据范围

输入字符串长度 $[0,25]$。
字符串中不含空格。

样例：

输入: "0"

输出: true

模拟法 $O(n)$

难顶的模拟题

class Solution {
public:
  bool isNumber(string s) {
    // 1.去除开头和结尾的空格
    int i = 0, j = s.size() - 1;
    while (i < s.size() && s[i] == ' ') i++;
    while (j >= 0 && s[j] == ' ') j--;
    if (i > j) return false;
    s = s.substr(i, j - i + 1);
    
    // 2.去除开头的 + 和 - (去除后在循环中只用判断数字、点、e/E 3种情况)
    if (s[0] == '+' || s[0] == '-') s = s.substr(1);
    if (s.size() == 1 && s[0] == '.') return false;
    
    int dot = 0, e = 0;
    for (int i = 0; i < s.size(); i++) {
      if (s[i] >= '0' && s[i] <= '9') {
        continue;  // 字符, 而非数字
      } else if (s[i] == '.') {
        dot++;
        if (dot > 1 || e) return false;
      } else if (s[i] == 'e' || s[i] == 'E') {
        e++;
        if (!i || i == s.size() - 1 || (i == 1 && s[0] == '.') || e > 1) return false;
        if (i + 1 < s.size() && (s[i + 1] == '-' || s[i + 1] == '+')) {
          if (i + 1 == s.size() - 1) return false;
          i++;
        }
      } else {  // 中间若包含其他字符，则ret false('e'后接'+/-'的情况在'e'中处理)
        return false;
      }
    }
    return true;
  }
};

调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序。

使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分。

数据范围

数组长度 $[0,100]$。

样例

输入：[1,2,3,4,5]

输出: [1,3,5,2,4]

循环遍历 $O(n)$

class Solution {
public:
  void reOrderArray(vector<int> &array) {
    int l = 0, r = array.size() - 1;
    while (l < r) {
      while (l < r && array[l] % 2 == 1) l++;
      while (l < r && array[r] % 2 == 0) r--;
      swap(array[l], array[r]);
    }
  }
};

链表中倒数第k个节点

输入一个链表，输出该链表中倒数第 $k$ 个结点。

注意：

• k >= 1;
• 如果 $k$ 大于链表长度，则返回 NULL;

数据范围

链表长度 $[0,30]$。

样例

输入：链表：1->2->3->4->5 ，k=2

输出：4

法1 1-pass with 快慢指针 $O(n)$

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode* findKthToTail(ListNode* pListHead, int k) {
    ListNode *fast = pListHead, *slow = pListHead;
    while (k--) {
      if (fast) {
        fast = fast->next;
      } else {
        return nullptr;
      }
    }
    while (fast) {
      fast = fast->next;
      slow = slow->next;
    }
    return slow;
  }
};

法2 2-pass $O(n)$

class Solution {
public:
  ListNode* findKthToTail(ListNode* pListHead, int k) {
    int s = 0;
    for (auto p = pListHead; p; p = p->next) s++;
    if (s < k) return nullptr;
    auto p = pListHead;
    for (int i = 0; i < s - k; i++) p = p->next;
    return p;
  }
};

链表中环的入口结点★

给定一个链表，若其中包含环，则输出环的入口节点。

若其中不包含环，则输出null。

数据范围

节点 val 值取值范围 $[1,1000]$。
节点 val 值各不相同。
链表长度 $[0,500]$。

样例

给定如上所示的链表：
[1, 2, 3, 4, 5, 6]
2
注意，这里的2表示编号是2的节点，节点编号从0开始。所以编号是2的节点就是val等于3的节点。

则输出环的入口节点3.

法1 小学奥数 + 快慢指针扫描 $O(n)$

解析请看y总视频
看懂后以后遇到此题在草稿纸上自己应该能推导出来

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode *entryNodeOfLoop(ListNode *head) {
    // 防止只有1个元素的无环情况: 相遇后访问next语句会导致segment fault
    if (!head || !head->next) return nullptr;
    
    ListNode *fast = head, *slow = head;
    while (fast && slow) {
      fast = fast->next;
      slow = slow->next;
      if (fast) fast = fast->next;
      
      if (fast == slow) {
        slow = head;
        while (fast != slow) {
          fast = fast->next;
          slow = slow->next;
        }
        return fast;
      }
    }
    return nullptr;
  }
};

法2 使用哈希表或者set

与“快慢指针扫描法”相比，空间复杂度会高一些

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode *entryNodeOfLoop(ListNode *head) {
    unordered_set<ListNode*> us;
    auto p = head;
    while (p) {
      if (!us.count(p)) {
        us.insert(p);
        p = p->next;
      } else {
        return p;
      }
    }
    return nullptr;
  }
};

Week 3

反转链表★

定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。

思考题：

• 请同时实现迭代版本和递归版本。

数据范围

链表长度 $[0,30]$。

样例

输入:1->2->3->4->5->NULL

输出:5->4->3->2->1->NULL

法1 迭代法

翻转即将所有节点的next指针指向前驱节点。
由于是单链表，我们在迭代时不能直接找到前驱节点，所以我们需要一个额外的指针保存前驱节点。同时在改变当前节点的next指针前，不要忘记保存它的后继节点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode* reverseList(ListNode* head) {
    ListNode *cur = head, *prev = nullptr;
    while (cur) {
      ListNode *next = cur->next;
      cur->next = prev;
      prev = cur, cur = next;
    }
    return prev;
  }
};

法2 递归法

首先我们先考虑 reverseList() 函数能做什么，它可以翻转一个链表，并返回新链表的头节点，也就是原链表的尾节点。
所以我们可以先递归处理 reverseList(head->next)，这样我们可以将以``head->next`为头节点的链表翻转，此时head->next是新链表的尾节点，我们令它的next指针指向head，并将head->next指向空即可将整个链表翻转。

class Solution {
public:
  ListNode* reverseList(ListNode* head) {
    if (!head || !head->next) return head;
    ListNode *new_head = reverseList(head->next);
    head->next->next = head;
    head->next = nullptr;
    return new_head;
  }
};

合并两个排序的链表

输入两个递增排序的链表，合并这两个链表并使新链表中的结点仍然是按照递增排序的。

数据范围

链表长度 $[0,500]$。

样例

输入：1->3->5 , 2->4->5

输出：1->2->3->4->5->5

题解

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode* merge(ListNode* l1, ListNode* l2) {
    ListNode *dummy = new ListNode(-1), *cur = dummy;
    while (l1 && l2) {
      if (l1->val <= l2->val) {
        cur->next = l1;
        l1 = l1->next;
      } else {
        cur->next = l2;
        l2 = l2->next;
      }
      cur = cur->next;  // cur也要移动
    }
    cur->next = (l1? l1: l2);
    return dummy->next;
  }
};

树的子结构

输入两棵二叉树 $A，B$，判断 $B$ 是不是 $A$ 的子结构。

我们规定空树不是任何树的子结构。

数据范围

每棵树的节点数量 $[0,1000]$。

样例

树 $A$：

     8
    / \
   8   7
  / \
 9   2
    / \
   4   7

树 $B$：

   8
  / \
 9   2

返回 true，因为 $B$ 是 $A$ 的子结构。

递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  bool hasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
    // pRoot2为空不是任何树的子结构, pRoot1为空为终止条件
    if (!pRoot1 || !pRoot2) return false;
    if (dfs(pRoot1, pRoot2)) return true;
    return hasSubtree(pRoot1->left, pRoot2) || hasSubtree(pRoot1->right, pRoot2);
  }
  
  bool dfs(TreeNode *pRoot1, TreeNode *pRoot2) {
    if (!pRoot2) return true;
    if (!pRoot1 || pRoot1->val != pRoot2->val) return false;
    return dfs(pRoot1->left, pRoot2->left) && dfs(pRoot1->right, pRoot2->right);
  }
};

注意 dfs 不能写下面这个函数：

bool IsSame(TreeNode *A, TreeNode *B) {
  if (!A || !B) return !A && !B;
  return A->val == B->val && IsSame(A->left, B->left) && IsSame(A->right, B->right);
}

因为从本题给出的例子看出 “子结构” 并非要求完全一致（A树中的2还有两个儿子，而B树中2为叶子节点）。

二叉树的镜像

输入一个二叉树，将它变换为它的镜像。

数据范围

树中节点数量 $[0,100]$。

样例

输入树：
      8
     / \
    6  10
   / \ / \
  5  7 9 11

 [8,6,10,5,7,9,11,null,null,null,null,null,null,null,null] 
输出树：
      8
     / \
    10  6
   / \ / \
  11 9 7  5

 [8,10,6,11,9,7,5,null,null,null,null,null,null,null,null]

递归法

递归遍历原树的所有节点，将每个节点的左右儿子互换即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  void mirror(TreeNode* root) {
    if (!root) return;
    mirror(root->left);
    mirror(root->right);
    swap(root->left, root->right);
  }
};

对称的二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。

如果一棵二叉树和它的镜像一样，那么它是对称的。

数据范围

树中节点数量 $[0,100]$。

样例

如下图所示二叉树[1,2,2,3,4,4,3,null,null,null,null,null,null,null,null]为对称二叉树：
    1
   / \
  2   2
 / \ / \
3  4 4  3

如下图所示二叉树[1,2,2,null,4,4,3,null,null,null,null,null,null]不是对称二叉树：
    1
   / \
  2   2
   \ / \
   4 4  3

递归法

两个子树互为镜像当且仅当：

1. 两个子树的根节点值相等；
2. 第一棵子的左子树和第二棵子树的右子树互为镜像，且第一棵子树的右子树和第二棵子树的左子树互为镜像；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  bool isSymmetric(TreeNode* root) {
    if (!root) return true;
    return dfs(root->left, root->right);
  }
  
  bool dfs(TreeNode *p, TreeNode *q) {
    if (!p || !q) return !p && !q;
    return p->val == q->val && dfs(p->left, q->right) && dfs(p->right, q->left);
  }
};

顺时针打印矩阵★

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

数据范围

矩阵中元素数量 $[0,400]$。

样例

输入：
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]

输出：[1,2,3,4,8,12,11,10,9,5,6,7]

模拟法

走到头，或者走到已经走过的地方就掉头。

class Solution {
public:
  vector<int> printMatrix(vector<vector<int> > matrix) {
    vector<int> res;
    if (matrix.empty()) return res;
    
    int n = matrix.size(), m = matrix[0].size();
    vector<vector<bool>> st(n, vector<bool>(m, false));
    int x = 0, y = 0, d = 1, a, b;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    for (int i = 0; i < n * m; i++) {
      res.push_back(matrix[x][y]);
      st[x][y] = true;
      
      a = x + dx[d], b = y + dy[d];
      if (a >= n || a < 0 || b >= m || b < 0 || st[a][b]) {  // st[a][b]必须放最后, 否则可能访问出界
        d = (d + 1) % 4;
        a = x + dx[d], b = y + dy[d];
      }
      x = a, y = b;
    }
    return res;
  }
};

包含min函数的栈★

设计一个支持push，pop，top等操作并且可以在O(1)时间内检索出最小元素的堆栈。

• push(x)–将元素x插入栈中
• pop()–移除栈顶元素
• top()–得到栈顶元素
• getMin()–得到栈中最小元素

数据范围

操作命令总数 $[0,100]$。

样例

MinStack minStack = new MinStack();
minStack.push(-1);
minStack.push(3);
minStack.push(-4);
minStack.getMin();   --> Returns -4.
minStack.pop();
minStack.top();      --> Returns 3.
minStack.getMin();   --> Returns -1.

辅助栈

我们除了维护基本的栈结构之外，还需要维护一个单调栈，来实现返回最小值的操作。
下面介绍如何维护单调栈：

• 当我们向栈中压入一个数时，如果该数 ≤≤ 单调栈的栈顶元素，则将该数同时压入单调栈中；否则，不压入，这是由于栈具有先进后出性质，所以在该数被弹出之前，栈中一直存在一个数比该数小，所以该数一定不会被当做最小数输出。
• 当我们从栈中弹出一个数时，如果该数等于单调栈的栈顶元素，则同时将单调栈的栈顶元素弹出。
• 单调栈由于其具有单调性，所以它的栈顶元素，就是当前栈中的最小数。

class MinStack {
public:
  stack<int> stk, min_stk;
  
  /** initialize your data structure here. */
  MinStack() {
      
  }
  
  void push(int x) {
    stk.push(x);
    // 当 x = min_stk.top() 时也应当push进min_stk
    if (min_stk.empty() || x <= min_stk.top()) min_stk.push(x);
  }
  
  void pop() {
    if (stk.top() == min_stk.top()) min_stk.pop();
    stk.pop();
  }
  
  int top() {
    return stk.top();
  }
  
  int getMin() {
    return min_stk.top();
  }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

栈的压入、弹出序列★

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。

假设压入栈的所有数字均不相等。

例如序列 $1,2,3,4,5$ 是某栈的压入顺序，序列 $4,5,3,2,1$ 是该压栈序列对应的一个弹出序列，但 $4,3,5,1,2$ 就不可能是该压栈序列的弹出序列。

注意：若两个序列长度不等则视为并不是一个栈的压入、弹出序列。若两个序列都为空，则视为是一个栈的压入、弹出序列。

数据范围

序列长度 $[0,1000]$。

样例

输入：[1,2,3,4,5]
      [4,5,3,2,1]

输出：true

模拟法

栈只有push()和pop()两个操作会影响栈中的数据

若栈顶元素 = 弹出序列首部, 则必然对应pop(); 否则, 则必然要将数据push进去

class Solution {
public:
  bool isPopOrder(vector<int> pushV,vector<int> popV) {
    if (pushV.size() != popV.size()) return false;
    
    stack<int> stk;
    int index = 0;
    for (auto x: pushV) {
      stk.push(x);
      while (stk.size() && stk.top() == popV[index]) {
        stk.pop();
        index++;
      }
    }
    return stk.empty()? true: false;
  }
};

不分行从上往下打印二叉树

从上往下打印出二叉树的每个结点，同一层的结点按照从左到右的顺序打印。

数据范围

树中节点的数量 $[0,1000]$。

样例

输入如下图所示二叉树[8, 12, 2, null, null, 6, null, 4, null, null, null]
    8
   / \
  12  2
     /
    6
   /
  4

输出：[8, 12, 2, 6, 4]

BFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  vector<int> printFromTopToBottom(TreeNode* root) {
    vector<int> res;
    if (!root) return res;
    
    queue<TreeNode*> q;
    q.push(root);
    while (q.size()) {
      auto t = q.front();
      q.pop();
      res.push_back(t->val);
      
      if (t->left) q.push(t->left);
      if (t->right) q.push(t->right);
    }
    return res;
  }
};

分行从上往下打印二叉树★

从上到下按层打印二叉树，同一层的结点按从左到右的顺序打印，每一层打印到一行。

数据范围

树中节点的数量 $[0,1000]$。

样例

输入如下图所示二叉树[8, 12, 2, null, null, 6, null, 4, null, null, null]
    8
   / \
  12  2
     /
    6
   /
  4

输出：[[8], [12, 2], [6], [4]]

BFS + 每层放null

在每层结束处加上null标志, 读到null时意味该层结束, 将该层结果保存, 并且此时下一层节点已全入队, 应此再入队下一层标志null

如果不是null就将当前节点值放入level, 并且左右子树若存则入队

class Solution {
public:
  vector<vector<int>> printFromTopToBottom(TreeNode* root) {
    if (!root) return res;
    vector<vector<int>> res;

    
    queue<TreeNode*> q;
    q.push(root);
    q.push(nullptr);
    vector<int> level;
    while (q.size()) {
      auto t = q.front();
      q.pop();
      
      if (t) {
        level.push_back(t->val);
        if (t->left) q.push(t->left);
        if (t->right) q.push(t->right);
      } else {
        if (q.size()) q.push(nullptr);
        res.push_back(level);
        level.clear();
      }
    }
    return res;
  }
};

之字形打印二叉树★

请实现一个函数按照之字形顺序从上向下打印二叉树。

即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

数据范围

树中节点的数量 $[0,1000]$。

样例

输入如下图所示二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]
    8
   / \
  12  2
     / \
    6   4
输出：[[8], [2, 12], [6, 4]]

BFS + 每层补充null + flag翻转每层结果

在将level压入到res前，进行reverse(level.begin(), level.end())是最便捷的。

class Solution {
public:
  vector<vector<int>> printFromTopToBottom(TreeNode* root) {
    if (!root) return res;
    vector<vector<int>> res;
    
    queue<TreeNode*> q;
    q.push(root);
    q.push(nullptr);
    vector<int> level;
    bool flag = false;
    while (q.size()) {
      auto t = q.front();
      q.pop();
      
      if (t) {
        level.push_back(t->val);
        if (t->left) q.push(t->left);
        if (t->right) q.push(t->right);
      } else {
        if (q.size()) q.push(nullptr);
        if (flag) reverse(level.begin(), level.end());
        flag = !flag;
        res.push_back(level);
        level.clear();
      }
    }
    return res;
  }
};

Week 4

二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。

如果是则返回true，否则返回false。

假设输入的数组的任意两个数字都互不相同。

数据范围

数组长度 $[0,1000]$。

样例

输入：[4, 8, 6, 12, 16, 14, 10]

输出：true

递归法

class Solution {
public:
  vector<int> seq_;
  
  bool verifySequenceOfBST(vector<int> sequence) {
    seq_ = sequence;
    return dfs(0, seq_.size() - 1);
  }
  
  bool dfs(int l, int r) {
    if (l >= r) return true;
    int k = l;
    while (k < r && seq_[k] < seq_[r]) k++;
    for (int i = k; i < r; i++) {
      if (seq_[i] <= seq_[r]) return false;
    }
    return dfs(l, k - 1) && dfs(k, r - 1);  // k是右子树起点
  }
};

二叉树中和为某一值的路径★

输入一棵二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。

从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

保证树中结点值均不小于 $0$。

数据范围

树中结点的数量 $[0,1000]$。

样例

给出二叉树如下所示，并给出num=22。
      5
     / \
    4   6
   /   / \
  12  13  6
 /  \    / \
9    1  5   1

输出：[[5,4,12,1],[5,6,6,5]]

递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  vector<vector<int>> res_;
  
  vector<vector<int>> findPath(TreeNode* root, int sum) {
    vector<int> path;
    dfs(root, sum, path);
    return res_;
  }
  
  void dfs(TreeNode *root, int sum, vector<int> &path) {
    if (!root) return;
    // if (!root && !sum) res_.push_back(path);  // 不能放这, 叶子节点的2个null儿子都会触发
    path.push_back(root->val);
    sum -= root->val;
    
    if (!sum && !root->left && !root->right) res_.push_back(path);
    dfs(root->left, sum, path);
    dfs(root->right, sum, path);
    
    path.pop_back();
    sum += root->val;
  }
};

复杂链表的复刻★

请实现一个函数可以复制一个复杂链表。

在复杂链表中，每个结点除了有一个指针指向下一个结点外，还有一个额外的指针指向链表中的任意结点或者null。

注意：

• 函数结束后原链表要与输入时保持一致。

数据范围

链表长度 $[0,500]$。

法1 hash表法(推荐)

问题难点在于random的处理：若搜到有random时就new一个对应节点，则后续节点的next对应到这个节点时不好处理，因此可以用hash表，使得：

当节点1的random和节点2的next对应节点相同时(key相同)时，新链表中对应的节点1’的random和节点2’的next对应的节点也能相同(value相同)

hash的是node 和 node->random

/**
 * Definition for singly-linked list with a random pointer.
 * struct ListNode {
 *     int val;
 *     ListNode *next, *random;
 *     ListNode(int x) : val(x), next(NULL), random(NULL) {}
 * };
 */
class Solution {
public:
  ListNode *copyRandomList(ListNode *head) {
    unordered_map<ListNode*, ListNode*> hash;
    hash[nullptr] = nullptr;
    auto dummy = new ListNode(-1), cur = dummy;
    
    while (head) {
      // hash的是 head 和 head->random
      if (!hash.count(head)) hash[head] = new ListNode(head->val);
      if (!hash.count(head->random)) hash[head->random] = new ListNode(head->random->val);
      
      cur->next = hash[head];
      cur->next->random = hash[head->random];
      
      head = head->next;
      cur = cur->next;
    }
    return dummy->next;
  }
};

法2 并行链表

class Solution {
public:
    ListNode *copyRandomList(ListNode *head) {
        // 1. 链表所有节点中间都插入一个复制节点，作为并行链表
        for (auto p = head; p; ) {
            ListNode* np = new ListNode(p->val);
            np->next = p->next;
            p->next = np;
            p = np->next;
        }

        // 2. 遍历新链表，遇到Random节点后对应改变并行链表中的节点
        for (auto p = head; p; p = p->next->next) {
            if (p->random) {
                p->next->random = p->random->next;
            }
        }

        // 3. 提取出并行链表
        // 注意这里要实现的链表的复刻：原链表应恢复为原来的结构(前面已经修改了原链表的结构)
        // p指向原链表的节点, cur指向并行链表的节点
        auto dummy = new ListNode(-1), cur = dummy;
        for (auto p = head; p; p = p->next) {
            cur->next = p->next;
            cur = cur->next;
            p->next = p->next->next;
        }
        return dummy->next;
    }
};

二叉搜索树与双向链表★

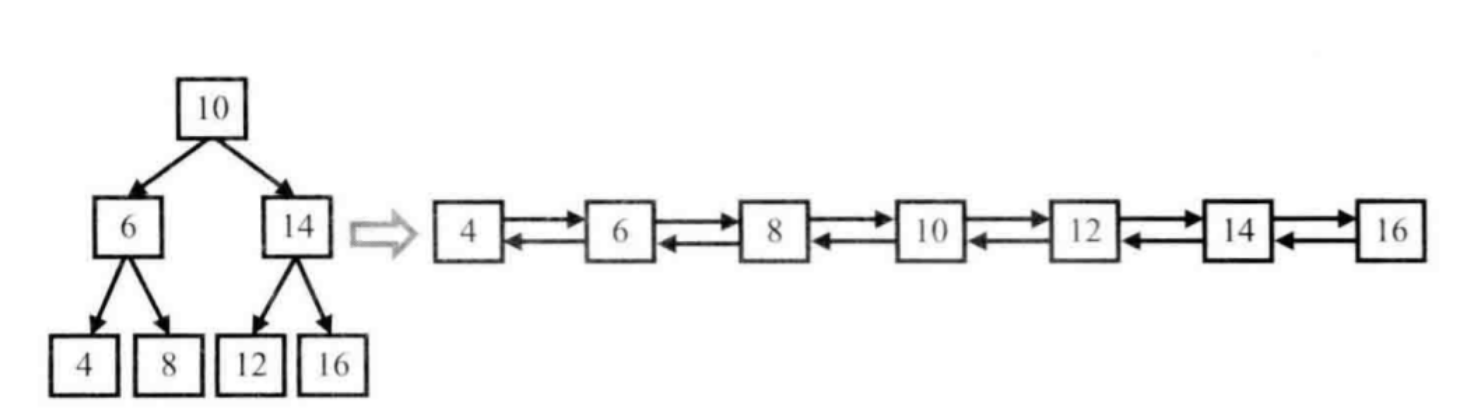
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。

要求不能创建任何新的结点，只能调整树中结点指针的指向。

注意：

• 需要返回双向链表最左侧的节点。

例如，输入下图中左边的二叉搜索树，则输出右边的排序双向链表。

数据范围

树中节点数量 $[0,500]$。

法1 修改的中序优先遍历

就在中序递归遍历的基础上改了一点点，用一个pre指针保存中序遍历的前一个结点。
因为是中序遍历，遍历顺序就是双线链表的建立顺序；
每一个结点访问时它的左子树肯定被访问过了，所以放心大胆的改它的left指针，不怕树断掉；
同理，pre指向的结点保存的数肯定小于当前结点，所以其左右子树肯定都访问过了，所以其right指针也可以直接改。

最后需要一直向左找到双向链表的头结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  TreeNode* prev = nullptr;
  
  TreeNode* convert(TreeNode* root) {
    dfs(root);
    while (root && root->left) root = root->left;
    return root;
  }
  
  void dfs(TreeNode *root) {
    if (!root) return;
    dfs(root->left);
    
    root->left = prev;
    if (prev) prev->right = root;
    prev = root;
    
    dfs(root->right);
  }
};

法2 递归法

class Solution {
public:
  TreeNode* convert(TreeNode* root) {
    if (!root) return nullptr;
    auto sides = dfs(root);
    return sides.first;
  }

  pair<TreeNode*, TreeNode*> dfs(TreeNode *root) {
    if (!root->left && !root->right) return {root, root};
    
    if (root->left && root->right) {
      auto lsides = dfs(root->left), rsides = dfs(root->right);
      lsides.second->right = root, root->left = lsides.second;
      rsides.first->left = root, root->right = rsides.first;
      return {lsides.first, rsides.second};
    }
    
    if (root->left) {
      auto lsides = dfs(root->left);
      lsides.second->right = root, root->left = lsides.second;
      return {lsides.first, root};
    }
    
    if (root->right) {
      auto rsides = dfs(root->right);
      rsides.first->left = root, root->right = rsides.first;
      return {root, rsides.second};
    }
  }
};

序列化二叉树★★

请实现两个函数，分别用来序列化和反序列化二叉树。

您需要确保二叉树可以序列化为字符串，并且可以将此字符串反序列化为原始树结构。

数据范围

树中节点数量 $[0,1000]$。

样例

你可以序列化如下的二叉树
    8
   / \
  12  2
     / \
    6   4

为："[8, 12, 2, null, null, 6, 4, null, null, null, null]"

注意:

• 以上的格式是AcWing序列化二叉树的方式，你不必一定按照此格式，所以可以设计出一些新的构造方式。

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

  // Encodes a tree to a single string.
  string serialize(TreeNode* root) {
    string res;
    dfs_s(root, res);
    return res;
  }
  
  void dfs_s(TreeNode *root, string &s) {  // 必须加引用
    if (!root) {
      s += "null ";
      return;
    }
    s += to_string(root->val) + ' ';
    dfs_s(root->left, s);
    dfs_s(root->right, s);
  }

  // Decodes your encoded data to tree.
  TreeNode* deserialize(string data) {
    int u = 0;
    auto root = dfs_d(data, u);
    return root;
  }
  
  TreeNode *dfs_d(string &data, int &u) {  // 必须加引用
    if (u == data.size()) return nullptr;
    
    int k = u;
    while (data[k] != ' ') k++;  // 只能用单引号
    if (data[u] == 'n') {
      u = k + 1;
      return nullptr;
    }
    
    int num = 0, sign = 1;
    if (data[u] == '-') {
      sign = -1;
      u++;
    }
    for (int i = u; i < k; i++)
      num = 10 * num + data[i] - '0';
    num = sign * num;
    u = k + 1;
    
    auto root = new TreeNode(num);
    root->left = dfs_d(data, u);  // 只有u是引用，不能传局部变量k + 1
    root->right = dfs_d(data, u);
    return root;
  }
};

若不使用单引号，报错信息如下：

Line 40: Char 20: warning: result of comparison against a string literal is unspecified (use an explicit string comparison function instead) [-Wstring-compare]
    while (data[k] != " ") k++;
                   ^  ~~~
Line 40: Char 20: error: comparison between pointer and integer ('__gnu_cxx::__alloc_traits<std::allocator<char>, char>::value_type' (aka 'char') and 'const char *')
    while (data[k] != " ") k++;
           ~~~~~~~ ^  ~~~
1 warning and 1 error generated.

数字排列★

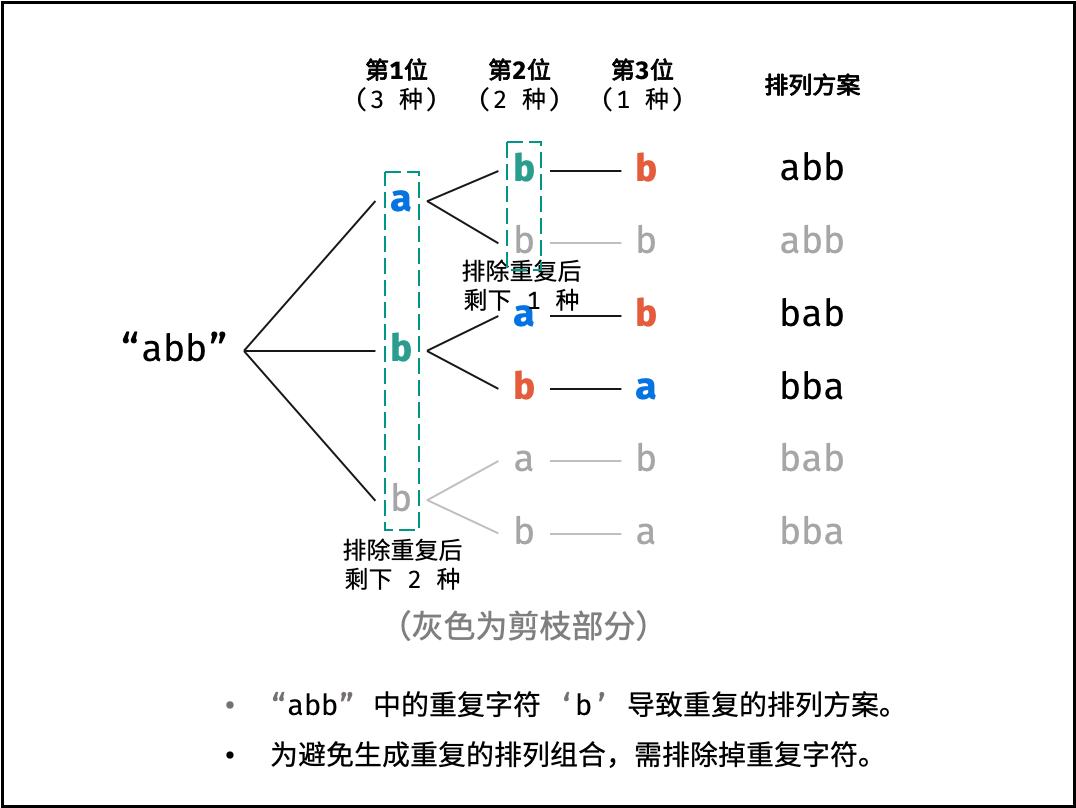
输入一组数字（可能包含重复数字），输出其所有的排列方式。

数据范围

输入数组长度 $[0,6]$。

样例

输入：[1,2,3]

输出：
      [
        [1,2,3],
        [1,3,2],
        [2,1,3],
        [2,3,1],
        [3,1,2],
        [3,2,1]
      ]

dfs暴搜

其实更推荐后面一题的写法。

思路是暴搜, 但是需要处理重复元素

1. 将所有数排序, 这样相同的数会排在一起
2. 从小到大枚举每个数, 每次将它放在一个空位上
3. 对于相同数, 其选择空位的起始位置start并不等于0, 而是必须在前一个数位置后面
4. 注意回溯, 但dfs使用state进行传值时不用手动处理

class Solution {
public:
  vector<vector<int>> res_;
  vector<int> path_;
  vector<int> nums_;
  
  vector<vector<int>> permutation(vector<int>& nums) {
    nums_ = nums;
    path_.resize(nums_.size());
    sort(nums_.begin(), nums_.end());
    dfs(0, 0, 0);
    return res_;
  }
  
  // u为枚举nums的下标, start为nums[u]可选起始位置(是否为重复元素会有影响), state记录path空位情况
  void dfs(int u, int start, int state) {
    if (u == nums_.size()) {
      res_.push_back(path_);
      return;
    }
    if (!u || nums_[u] != nums_[u - 1]) start = 0;
    for (int i = start; i < nums_.size(); i++) {
      if (!(state >> i & 1)) {  // &, 而非&&
        path_[i] = nums_[u];
        dfs(u + 1, i + 1, state + (1 << i));  // start传的是i + 1
      }
    }
  }
};

字符串的排列

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

回溯法

具体参考：剑指 Offer 38. 字符串的排列（回溯法，清晰图解）

set 加入元素的函数为 insert()

class Solution {
public:
  vector<string> res_;

  vector<string> permutation(string s) {
    dfs(s, 0);
    return res_;
  }

  void dfs(string &s, int u) {
    if (u == s.size() - 1) {
      res_.push_back(s);
      return;
    }
    set<int> st;
    for (int i = u; i < s.size(); i++) {
      if (st.find(s[i]) != st.end()) continue;
      st.insert(s[i]);
      swap(s[i], s[u]);
      dfs(s, u + 1);
      swap(s[i], s[u]);
    }
  }
};

数组中出现次数超过一半的数字★

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

假设数组非空，并且一定存在满足条件的数字。

思考题：

• 假设要求只能使用 $O(n)$ 的时间和额外 $O(1)$ 的空间，该怎么做呢？

数据范围

数组长度 $[1,1000]$。

样例

输入：[1,2,1,1,3]

输出：1

题解

排序可以解决该问题: 中间的数一定是目标数, 但时间复杂度过高
本题思路:
初始化cnt = 0, val 为一不存在nums中的数
val = target使得对应于target的cnt++
val != target使得对应于target的cnt-- (对应非target的cnt++, 等价对应于target的cnt–)
由于target数量大于总数的一半, 最后剩下的val = target

吐槽一句：代码是按照google style c++写出来的，本题的代码有点丑呀🥵！

class Solution {
public:
  int moreThanHalfNum_Solution(vector<int>& nums) {
    int val = -1, cnt = 0;
    for (auto x: nums) {
      if (x == val) {
        cnt++;
      } else {
        if (cnt) {
          cnt--;
        } else {
          val = x;
          cnt = 1;
        }
      }
    }
    return val;
  }
};

最小的k个数

输入 $n$ 个整数，找出其中最小的 $k$ 个数。

注意：

• 输出数组内元素请按从小到大顺序排序;

数据范围

$1 \le k \le n \le 1000$

样例

输入：[1,2,3,4,5,6,7,8] , k=4

输出：[1,2,3,4]

法1. 堆排序

时间复杂度: $O(n\cdot logk)$, 每次插入的时间复杂度为 $O(logk)$
维护一个大小为k的大根堆，将数组元素都push进堆，当堆中的数大于k时弹出堆顶元素。注意弹出堆顶的顺序是从大到小的k个数，要进行逆序操作。

大根堆 可以通过查看堆头heap.top()，快速知道堆中的最大元素。
小根堆 的声明为 priority_queue<int, vector<int>, greater<int>>
heap 加入元素的函数为 push()

class Solution {
public:
  vector<int> getLeastNumbers_Solution(vector<int> input, int k) {
    vector<int> res;
    // if (!k) return res;  // 如果k=0没有这句的话，当heap为空访问heap.top()时报seg fault 
    priority_queue<int> heap;  // 大根堆
    for (auto x: input) {
      if (heap.size() < k || heap.top() > x) heap.push(x);
      if (heap.size() > k) heap.pop();
    }
    while (heap.size()) {
      res.push_back(heap.top());
      heap.pop();
    }
    reverse(res.begin(), res.end());
    return res;
  }
};

法2: k次快选

时间复杂度: $k\cdot log(n)$

class Solution {
public:
  vector<int> input_;
  vector<int> getLeastNumbers_Solution(vector<int> input, int k) {
    input_ = input;
    vector<int> res;
    for (int i = 1; i <= k; i++) {
      res.push_back(quick_choose(0, input_.size() - 1, i));
    }
    return res;
  }
  
  int quick_choose(int l, int r, int k) {
    if (l >= r) return input_[l];
    int i = l - 1, j = r + 1, x = input_[(i + r) >> 1];
    while (i < j) {
      while (input_[++i] < x) {};
      while (input_[--j] > x) {};
      if (i < j) swap(input_[i], input_[j]);
    }
    if (k <= j - l + 1) return quick_choose(l, j, k);  // 必须是<=
    return quick_choose(j + 1, r, k - (j - l + 1));
  }
};

数据流中的中位数★

如何得到一个数据流中的中位数？

如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。

如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

数据范围

数据流中读入的数据总数 $[1,1000]$。

样例

输入：1, 2, 3, 4

输出：1,1.5,2,2.5

解释：每当数据流读入一个数据，就进行一次判断并输出当前的中位数。

题解 用一个小根堆min_heap维护较大的数, 用一个大根堆max_heap维护较小的数

那么中位数就可以用大小根堆的根节点进行表示

insert()插入一个新值时:

1. 先放入大根堆max_heap中
2. 如果max_heap的根 > min_heap的根, 则进行交换
3. 如果max_heap的数量比min_heap数量大1以上, 则将max_heap的队头放入min_heap中

返回的是double, 切勿用移位来求平均，而是应当用/ 2.0

class Solution {
public:
  priority_queue<int, vector<int>, greater<int>> min_heap;  // 小根堆
  priority_queue<int> max_heap;
  
  void insert(int num){
    max_heap.push(num);
    
    if (min_heap.size() && max_heap.top() > min_heap.top()) {
      auto maxv = max_heap.top(), minv = min_heap.top();
      max_heap.pop(), min_heap.pop();
      min_heap.push(maxv), max_heap.push(minv);
    }
    
    if (max_heap.size() - min_heap.size() > 1) {
      min_heap.push(max_heap.top());
      max_heap.pop();
    }
  }

  double getMedian(){
    if (max_heap.size() > min_heap.size()) return max_heap.top();
    return (max_heap.top() + min_heap.top()) / 2.0;  // 返回的是double, 必用2.0, 切勿用移位
  }
};

连续子数组的最大和

输入一个 非空 整型数组，数组里的数可能为正，也可能为负。

数组中一个或连续的多个整数组成一个子数组。

求所有子数组的和的最大值。

要求时间复杂度为 $O(n)$。

数据范围

数组长度 $[1,1000]$。
数组内元素取值范围 $[-200,200]$。

样例

输入：[1, -2, 3, 10, -4, 7, 2, -5]

输出：18

DP

使用s记录紧邻x的前面的连续数组最大和, 那么到x时:

1. 如果s大于等于0, 以x结尾的连续数组最大和为 x + s;
2. 如果s小于0, 以x结尾的连续数组最大和为x (前面是负数, 就没必要加上了);

可以使用INT_MIN 和 INT_MAX之类的。

class Solution {
public:
  int maxSubArray(vector<int>& nums) {
    int res = INT_MIN, s = 0;
    for (auto x: nums) {
      if (s > 0) {
        s = s + x;
      } else {
        s = x;
      }
      res = max(res, s);
    }
    return res;
  }
};

从1到n整数中1出现的次数★

输入一个整数 $n$，求从 $1$ 到 $n$ 这 $n$ 个整数的十进制表示中 $1$ 出现的次数。

例如输入 $12$，从 $1$ 到 $12$ 这些整数中包含 $“1”$ 的数字有 $1，10，11$ 和 $12$，其中 $“1”$ 一共出现了 $5$ 次。

数据范围

$1 \le n \le 10^9$

样例

输入： 12
输出： 5

题解

class Solution {
public:
  int numberOf1Between1AndN_Solution(int n) {
    int res = 0, dgt = GetDigit(n);
    for (int j = dgt - 1; ~j; j--) {
      int p = pow(10, j);
      // 不能在此函数中通过 vector<int> nums的size()求dgt: 求nums过程中n会被归0
      int left = n / p / 10, right = n % p, dj = n / p % 10;
      res += left * p;
      if (dj > 1) {
        res += p;
      } else if (dj == 1) {
        res += right + 1;
      }
    }
    return res;
  }
  
  int GetDigit(int n) {
    int res = 0;
    while (n) {
      res++;
      n /= 10;
    }
    return res;
  }
};

Week 5

数字序列中某一位的数字★

数字以 $0123456789101112131415…$ 的格式序列化到一个字符序列中。

在这个序列中，第 $5$ 位（从 $0$ 开始计数）是 $5$，第 $13$ 位是 $1$，第 $19$ 位是 $4$，等等。

请写一个函数求任意位对应的数字。

数据范围

$0 \le$ 输入数字 $\le 2147483647$

样例

输入：13

输出：1

题解

转化问题：
数字字符序列为12345678910…，第1位为1 （对于0特判，直接返回0）
这个问题的返回结果与原问题相同，这样等价处理的好处是：对于1位数来说，其个数为9，与n位数的情况能统一起来，这样写出来的代码更简洁

思路

1. 确定是i位数字: n - 1 * 9 - 2 * 90 - 3 * 900 …
2. 确定是i位数字的第几个, 即确定具体number
   比如从base=1000开始的4位, 第(n=4)/3上取整=2, 则number = base + [n/i] - 1 = 101 (向上取整)
3. 属于number的第几位
   注意取余数时, 如果n%i == 0, 则应当对应r = i位, 比如1012的第4位是2 (4%4=0)
4. 求number的第r位是多少
   比如12345的r = 2，那么就需要将小数点向右移动5-2=3位，然后通过% 10求此时个位数数字

class Solution {
public:
  int digitAtIndex(int n) {
    if (!n) return 0;
    long long dgt = 1, start = 1, count = 9; // long long
    while (n > dgt * count) {  // dgt * count才是dgt位数占的总位数
      n -= dgt * count;
      dgt++;
      start *= 10;
      count *= 10;
    }
    int num = start + (n + dgt - 1) / dgt - 1; // 向上取整数 + 第i个数是start + i - 1
    int r = (n % dgt)? (n % dgt): dgt;
    for (int j = 0; j < dgt - r; j++) num /= 10;
    return num % 10;
  }
};

把数组排成最小的数★

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

例如输入数组 $[3, 32, 321]$，则打印出这 $3$ 个数字能排成的最小数字 $321323$。

数据范围

数组长度 $[0,500]$。

样例

输入：[3, 32, 321]

输出：321323

注意：输出数字的格式为字符串。

重写cmp函数

class Solution {
public:
  static bool cmp(string &s1, string &s2) {  // static
    return s1 + s2 <= s2 + s1; 
  }
  
  string printMinNumber(vector<int>& nums) {
    vector<string> nums_strs;
    for (auto x: nums) nums_strs.push_back(to_string(x));
    sort(nums_strs.begin(), nums_strs.end(), cmp);  // cmp
    string res;
    for (auto x: nums_strs) res += x;
    return res;
  }
};

把数字翻译成字符串

给定一个数字，我们按照如下规则把它翻译为字符串：

$0$ 翻译成 a，$1$ 翻译成 b，……，$11$ 翻译成 l，……，$25$ 翻译成 z。

一个数字可能有多个翻译。

例如 $12258$ 有 $5$ 种不同的翻译，它们分别是 bccfi、bwfi、bczi、mcfi 和 mzi。

请编程实现一个函数用来计算一个数字有多少种不同的翻译方法。

数据范围

输入数字位数 $[1,101]$。

样例

输入："12258"

输出：5

DP

状态表示 f[i]:前i位数字有多少种不同的表示方法

状态计算 f[i] = f[i - 1] + f[i - 2]
前后分别对应将第i位数字单独翻译、 第i-1位和第i位一起进行翻译(必须合法:0~25且不能为05等, 即必须10~25)

边界情况 f[0] = 1: 让f[1]和f[2]数值正确

当 $num$ 第 $1, 2$ 位的组成的数字 ∈[10,25] 时，显然应有 2 种翻译方法，即 $dp[2] = dp[1] + dp[0] = 2$ ，而显然 $dp[1] = 1$ ，因此推出 $dp[0] = 1$ 。

class Solution {
public:
  int getTranslationCount(string s) {
    int n = s.size();
    vector<int> f(n + 1);
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
      f[i] = f[i - 1];
      int t = (i >= 2) * (10 * (s[i - 2] - '0') + s[i - 1] - '0');
      if (t >= 10 && t <= 25) f[i] += f[i - 2];
    }
    return f[n];
  }
};

礼物的最大价值

在一个 $m \times n$ 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 $0$）。

你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格直到到达棋盘的右下角。

给定一个棋盘及其上面的礼物，请计算你最多能拿到多少价值的礼物？

注意：

• $m, n \gt 0$
• $m \times n \le 1350$

样例：

输入：
[
  [2,3,1],
  [1,7,1],
  [4,6,1]
]

输出：19

解释：沿着路径 2→3→7→6→1 可以得到拿到最大价值礼物。

DP

class Solution {
public:
  int getMaxValue(vector<vector<int>> &grid) {
    int n = grid.size(), m = grid[0].size();
    vector<vector<int>> f(n + 1, vector<int>(m + 1, 0));
    for (int i = 1; i <= n; i++) {
      for (int j = 1; j <= m; j++) {
        f[i][j] = max(f[i - 1][j], f[i][j - 1]) + grid[i - 1][j - 1];
      }
    }
    return f[n][m];
  }
};

最长不含重复字符的子字符串★

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

假设字符串中只包含从 a 到 z 的字符。

数据范围

输入字符串长度 $[0,1000]$。

样例

输入："abcabc"

输出：3

双指针 + 利用hash快速查重

class Solution {
public:
  int longestSubstringWithoutDuplication(string s) {
    int res = 0;  // 用0不同特判s.empty()
    unordered_map<char, int> hash;
    for (int i = 0, j = 0; j < s.size(); j++) {
      hash[s[j]]++;
      while (hash[s[j]] > 1) hash[s[i++]]--;  // 不用i < j
      res = max(res, j - i + 1);
    }
    return res;
  }
};

丑数★

我们把只包含质因子 $2、3$ 和 $5$ 的数称作丑数（Ugly Number）。

例如 $6、8$ 都是丑数，但 $14$ 不是，因为它包含质因子 $7$。

求第 $n$ 个丑数的值。

数据范围

$1 \le n \le 1000$

样例

输入：5

输出：5

注意：习惯上我们把 $1$ 当做第一个丑数。

题解

考虑丑数集为S = 1, 2, 3, 4, 5, 6, 8, 9, 10, …

1. 包含因子2的S子集为S1, 则S1 / 2 = S （S1中元素因子只包含2、3、5, 除以一个2后只包含2、3、5, 就是一个丑集）
2. 包含因子3的S子集为S2, 则S2 / 3 = S
3. 包含因子5的S子集为S3, 则S3 / 5 = S

要求出S, 只需要对S1, S2, S3进行多路归并(注意去重)即可
利用S1 / 2 = S等性质, 我们不需要真的把S1, S2, S3求出来, 而可以这样做:
设置3个指针i,j和k, 2 * q[i], 3 * q[j]和5 * q[k]指向的就是S1, S2和S3中的最小元素。

吐槽：这一般没做的人谁能想到？

class Solution {
public:
  int getUglyNumber(int n) {
    vector<int> q;
    q.push_back(1);
    int i = 0, j = 0, k = 0;
    while (--n) {  // n-1次循环
      int t = min(2 * q[i], min(3 * q[j], 5 * q[k]));
      q.push_back(t);
      if (2 * q[i] == t) i++;
      if (3 * q[j] == t) j++;
      if (5 * q[k] == t) k++;
    }
    return q.back();   // 不能用q[n - 1], 此时n已为0
  }
};

字符串中第一个只出现一次的字符

在字符串中找出第一个只出现一次的字符。

如输入"abaccdeff"，则输出b。

如果字符串中不存在只出现一次的字符，返回 # 字符。

数据范围

输入字符串长度 $[0,1000]$。

样例：

输入："abaccdeff"

输出：'b'

hash表统计

class Solution {
public:
  char firstNotRepeatingChar(string s) {
    unordered_map<char, int> hash;
    for (auto x: s) hash[x]++;
    for (auto x: s) {
      if (hash[x] == 1) return x;
    }
    return '#';
  }
};

字符流中第一个只出现一次的字符

请实现一个函数用来找出字符流中第一个只出现一次的字符。

例如，当从字符流中只读出前两个字符 go 时，第一个只出现一次的字符是 g。

当从该字符流中读出前六个字符 google 时，第一个只出现一次的字符是 l。

如果当前字符流没有存在出现一次的字符，返回 # 字符。

数据范围

字符流读入字符数量 $[0,1000]$。

样例

输入："google"

输出："ggg#ll"

解释：每当字符流读入一个字符，就进行一次判断并输出当前的第一个只出现一次的字符。

双指针(队列) + hash表统计

时间复杂度为 $O(n)$

class Solution{
public:
  unordered_map<char, int> hash;
  queue<int> q;
  
  // void insert(char ch){
  //   q.push(ch);
  //   hash[ch]++;
  //   // 只是简单的pop, 没有hash对应数量的变化
  //   while (q.size() && hash[q.front()] > 1) q.pop();
  // }
  
  //Insert one char from stringstream
  void insert(char ch){
    // 优化: 只有insert导致重复出现才需要pop队头; 只有出现重复才有必要push(否则一定会被pop)
    if (++hash[ch] > 1) {
      while (q.size() && hash[q.front()] > 1) q.pop();
    } else {
      q.push(ch);
    }
  }
  
  //return the first appearence once char in current stringstream
  char firstAppearingOnce(){
    if(q.empty()) return '#';
    return q.front();
  }
};

数组中的逆序对★

在数组中的两个数字如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。

输入一个数组，求出这个数组中的逆序对的总数。

数据范围

给定数组的长度 $[0,100]$。

样例

输入：[1,2,3,4,5,6,0]

输出：6

基于归并排序的统计

通过归并排序, 时间复杂度由暴力做法的 $O(n^2)$ 减小到 $O(n \cdot logn)$

class Solution {
public:
  vector<int> nums_;
  int tmp[110];
  
  int merge(int l, int r) {
    if (l >= r) return 0;
    int mid = (l + r) >> 1;
    int res = merge(l, mid) + merge(mid + 1, r);
    
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
      if (nums_[i] <= nums_[j]) {  // 逆序对这必须 <=
        tmp[k++] = nums_[i++];
      } else {
        tmp[k++] = nums_[j++];
        res += mid - i + 1;
      }
    }
    while (i <= mid) tmp[k++] = nums_[i++];
    while (j <= r) tmp[k++] = nums_[j++];
    for (int i = l, j = 0; i <= r; i++, j++) nums_[i] = tmp[j];
    return res;
  }
  
  int inversePairs(vector<int>& nums) {
    nums_ = nums;
    return merge(0, nums_.size() - 1);
  }
};

两个链表的第一个公共结点

输入两个链表，找出它们的第一个公共结点。

当不存在公共节点时，返回空节点。

数据范围

链表长度 $[1,2000]$。
保证两个链表不完全相同，即两链表的头结点不相同。

样例

给出两个链表如下所示：
A：        a1 → a2
                   ↘
                     c1 → c2 → c3
                   ↗            
B:     b1 → b2 → b3

输出第一个公共节点c1

题解

有2种情况:

1. 存在公共节点, 设a1到公共节点距离为a, b1到公共节点距离为b, 公共段长度为c
   那么让两指针分别从a1, b1出发, 到达列表结尾处后分别从b1和a1重新出发
   则它们一定会在公共节点处相逢(走的路程 a + c + b = b + c + a)

2. 不存在公共节点, 设a1和b1到各自链表结尾的距离分别为a和b
   则使用1中方法, 它们一定也会同时到达结尾(走的路程为 a + b = b + a)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
  ListNode *findFirstCommonNode(ListNode *headA, ListNode *headB) {
    auto p = headA, q = headB;
    while (p != q) {
      if (p) {
        p = p->next;
      } else {
        p = headB;
      }
      
      if (q) {
        q = q->next;
      } else {
        q = headA;
      }
    }
    return p;
  }
};

数字在排序数组中出现的次数

统计一个数字在排序数组中出现的次数。

例如输入排序数组 $[1, 2, 3, 3, 3, 3, 4, 5]$ 和数字 $3$，由于 $3$ 在这个数组中出现了 $4$ 次，因此输出 $4$。

数据范围

数组长度 $[0,1000]$。

样例

输入：[1, 2, 3, 3, 3, 3, 4, 5] ,  3

输出：4

题解

使用二分法找到连续区间的上边界和下边界，这样才能保证时间复杂度为$O(log n)$
在工程中可以使用int num = count(nums.begin(), nums.end(), k);

class Solution {
public:
  int getNumberOfK(vector<int>& nums , int k) {
    if (nums.empty()) return 0;
    
    int l = 0, r = nums.size() - 1;
    while (l < r) {
      int mid = (l + r) >> 1;
      if (nums[mid] >= k) {
        r = mid;
      } else {
        l = mid + 1;
      }
    }
    int begin = l;
    
    l = 0, r = nums.size() - 1;
    while (l < r) {
      int mid = (l + r + 1) >> 1;
      if (nums[mid] <= k) {
        l = mid;  // 写到这马上给mid加1
      } else {
        r = mid - 1;
      }
    }
    
    return l - begin + 1;
  }
};

Week 6

0到n-1中缺失的数字

一个长度为 $n-1$ 的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围 $0$ 到 $n-1$ 之内。

在范围 $0$ 到 $n-1$ 的 $n$ 个数字中有且只有一个数字不在该数组中，请找出这个数字。

数据范围

$1 \le n \le 1000$

样例

输入：[0,1,2,4]

输出：3

二分法

class Solution {
public:
  int getMissingNumber(vector<int>& nums) {
    if (nums.empty()) return 0;
    int n_minus_1 = nums.size();
    if (nums.back() == n_minus_1 - 1) return n_minus_1;  // 确保能二分
    
    int l = 0, r = nums.size() - 1;
    while (l < r) {
      int mid = (l + r) >> 1;
      if (nums[mid] != mid) {
        r = mid;
      } else {
        l = mid + 1;
      }
    }
    return l;
  }
};

数组中数值和下标相等的元素

假设一个单调递增的数组里的每个元素都是整数并且是唯一的。

请编程实现一个函数找出数组中任意一个数值等于其下标的元素。

例如，在数组 $[-3, -1, 1, 3, 5]$ 中，数字 $3$ 和它的下标相等。

数据范围

数组长度 $[1,100]$。

样例

输入：[-3, -1, 1, 3, 5]

输出：3

注意:如果不存在，则返回-1。

二分法

class Solution {
public:
  int getNumberSameAsIndex(vector<int>& nums) {
    if (nums.empty()) return 0;
    int l = 0, r = nums.size() - 1;
    while (l < r) {
      int mid = (l + r) >> 1;
      if (nums[mid] >= mid) {
        r = mid;
      } else {
        l = mid + 1;
      }
    }
    if (nums[l] == l) return l;
    return -1;
  }
};

二叉搜索树的第k个结点★

给定一棵二叉搜索树，请找出其中的第 $k$ 小的结点。

你可以假设树和 $k$ 都存在，并且 $1≤k≤$ 树的总结点数。

数据范围

树中节点数量 $[1,500]$。

样例

输入：root = [2, 1, 3, null, null, null, null] ，k = 3

    2
   / \
  1   3

输出：3

dfs

对二叉树进行中序遍历，统计序列中第k位是啥。

扩展：如果是求 第k大的，只需要按照 右 - 自 - 左 顺序去找即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  int k_;
  TreeNode *res_;
  
  TreeNode* kthNode(TreeNode* root, int k) {
    k_ = k;
    dfs(root);
    return res_;
  }
  
  void dfs(TreeNode *root) {
    if (!root) return;
    dfs(root->left);
    if (!(--k_)) res_ = root;
    if (k_ > 0) dfs(root->right);
  }
};

不使用类的成员变量（效果与 全局变量 基本等价）的写法如下：

class Solution {
public:
  TreeNode* kthNode(TreeNode* root, int k) {
    TreeNode *res;
    dfs(root, k, &res);
    return res;
  }
  
  void dfs(TreeNode *root, int &k, TreeNode **res) {  // & 和 **
    if (!root) return;
    dfs(root->left, k);
    if (!(--i)) *res = root;
    if (k > 0) dfs(root->right, k);
  }
};

二叉树的深度

输入一棵二叉树的根结点，求该树的深度。

从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

数据范围

树中节点数量 $[0,500]$。

样例

输入：二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]如下图所示：
    8
   / \
  12  2
     / \
    6   4

输出：3

递归大法好

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  int treeDepth(TreeNode* root) {
    if (!root) return 0;
    return max(treeDepth(root->left), treeDepth(root->right)) + 1;
  }
};

平衡二叉树★

输入一棵二叉树的根结点，判断该树是不是平衡二叉树。

如果某二叉树中任意结点的左右子树的深度相差不超过 $1$，那么它就是一棵平衡二叉树。

注意：

• 规定空树也是一棵平衡二叉树。

数据范围

树中节点数量 $[0,500]$。

样例

输入：二叉树[5,7,11,null,null,12,9,null,null,null,null]如下所示，
    5
   / \
  7  11
    /  \
   12   9

输出：true

后序遍历，未剪枝

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  bool res_ = true;
  
  bool isBalanced(TreeNode* root) {
    dfs(root);
    return res_;
  }
  
  int dfs(TreeNode *root) {
    if (!root) return 0;
    int l = dfs(root->left), r = dfs(root->right);
    if (abs(l - r) > 1) res_ = false;
    return max(l, r) + 1;
  }
};

后序 + 剪枝

class Solution {
public:
  bool isBalanced(TreeNode* root) {
    return dfs(root) != -1;
  }

  int dfs(TreeNode *root) {
    if (!root) return 0;
    int depth_l = dfs(root->left);
    if (depth_l == -1) return -1;
    int depth_r = dfs(root->right);
    if (depth_r == -1) return -1;
    return (abs(depth_l - depth_r) <= 1)? max(depth_l, depth_r) + 1: -1;
  }
};

数组中只出现一次的两个数字★

一个整型数组里除了两个数字之外，其他的数字都出现了两次。

请写程序找出这两个只出现一次的数字。

你可以假设这两个数字一定存在。

数据范围

数组长度 $[1,1000]$。

样例

输入：[1,2,3,3,4,4]

输出：[1,2]

题解

4种位运算: &与 |或 ^异或 ~非

思路:

• 先将所有元素异或起来, 异或结果sum就为这2个只出现1次元素的异或
• 然后找到sum中某一位为1, 然后根据第k位是否为1将数组分成两部分
  由于这2个只出现1次的元素会被分开, 而出现两次的元素必定会被分到同一部分中
  因此这两部分都满足: 只有1个元素出现1次, 其他元素都出现2次

class Solution {
public:
  vector<int> findNumsAppearOnce(vector<int>& nums) {
    int sum = 0;
    for (auto x: nums) sum ^= x;
    int k = 0;
    while (!(sum >> k & 1)) k++;
    int first = 0;
    for (auto x: nums) {
      if (x >> k & 1) first ^= x;
    }
    return vector<int>{first, sum ^= first};
  }
};

数组中唯一只出现一次的数字★

在一个数组中除了一个数字只出现一次之外，其他数字都出现了三次。

请找出那个只出现一次的数字。

你可以假设满足条件的数字一定存在。

思考题：

• 如果要求只使用 $O(n)$ 的时间和额外 $O(1)$ 的空间，该怎么做呢？

数据范围

数组长度 $[1,1500]$。

样例

输入：[1,1,1,2,2,2,3,4,4,4]

输出：3

法1 按位统计

一共32个位，统计哪个位 1 出现次数 % 3 == 1，那么所求数该位为1，最后合起来就是答案。

时间复杂度 $O(32n)$
因为 n 一般在百万级别，$logn<32$，所以 $32n>nlogn$ ，不是严格的 $O(n)$

class Solution {
public:
  int findNumberAppearingOnce(vector<int>& nums) {
    int res = 0;
    for (int i = 0; i <= 31; i++) {
      int cnt = 0;
      for (auto x: nums) {
        if (x >> i & 1) cnt++;
      }
      if (cnt % 3) {
        res |= 1 << i;
      }
    }
    return res;
  }
};

法2 状态机

根据下面代码可以画出上面的状态机进行验证。

推导是根据真值表推导出状态转移方程，可参考：https://www.acwing.com/solution/content/19076/

class Solution {
public:
  int findNumberAppearingOnce(vector<int>& nums) {
    int ones = 0, twos = 0;
    for (auto x: nums) {
      ones = (ones ^ x) & ~twos;
      twos = (twos ^ x) & ~ones;
    }
    return ones;
  }
};

和为S的两个数字

输入一个数组和一个数字 $s$，在数组中查找两个数，使得它们的和正好是 $s$。

如果有多对数字的和等于 $s$，输出任意一对即可。

你可以认为每组输入中都至少含有一组满足条件的输出。

数据范围

数组长度 $[1,1002]$。

样例

输入：[1,2,3,4] , sum=7

输出：[3,4]

法1 双指针

时间复杂度：$O(n)$

空间复杂度：$O(1)$

class Solution {
public:
  vector<int> findNumbersWithSum(vector<int>& nums, int target) {
    int i = 0, j = nums.size() - 1;
    while (i < j) {
      if (nums[i] + nums[j] < target) {
        i++;
      } else if (nums[i] + nums[j] > target) {
        j--;
      } else {
        return vector<int>{nums[i], nums[j]};
      }
    }
    return vector<int>{};
  }
};

法2 hash表快速查找

时间复杂度：$O(n)$

空间复杂度：$O(n)$

class Solution {
public:
  vector<int> findNumbersWithSum(vector<int>& nums, int target) {
    unordered_map<int, int> hash;
    for (auto x: nums) {
      if (!hash[target - x]) {
        hash[x]++;
      } else {
        return vector<int>({x, target - x});
      }
    }
  }
};

和为S的连续正数序列

输入一个非负整数 $S$，打印出所有和为 $S$ 的连续正数序列（至少含有两个数）。

例如输入 $15$，由于 $1+2+3+4+5=4+5+6=7+8=15$，所以结果打印出 $3$ 个连续序列 $1 \sim 5$、$4 \sim 6$ 和 $7 \sim 8$。

数据范围

$0 \le S \le 1000$

样例

输入：15

输出：[[1,2,3,4,5],[4,5,6],[7,8]]

双指针

很多情况下，双指针和队列是等价的。
由于queue不支持遍历，所以这里还是用双指针吧。

分别用i和j表示连续序列的起止位置
如果采用暴力方法枚举i和j, 则时间复杂度为 $O(n^2)$
若利用规律: 当j右移时(加数个数增加), i一定也会右移, 则可写出时间复杂度为O(n)的算法

class Solution {
public:
  vector<vector<int> > findContinuousSequence(int sum) {
    vector<vector<int>> res;
    vector<int> path;
    for (int i = 1, j = 1, s = 0; j <= sum / 2 + 1; j++) {
      s += j;
      while (s > sum) {
        s -= i;
        i++;
      }
      if (s == sum && j - i + 1 >= 2) {  // 至少2个元素
        path.clear();
        for (int k = i; k <= j; k++) path.push_back(k);
        res.push_back(path);
      }
    }
    return res;
  }
};

翻转单词顺序

输入一个英文句子，单词之间用一个空格隔开，且句首和句尾没有多余空格。

翻转句子中单词的顺序，但单词内字符的顺序不变。

为简单起见，标点符号和普通字母一样处理。

例如输入字符串"I am a student."，则输出"student. a am I"。

数据范围

输入字符串长度 $[0,1000]$。

样例

输入："I am a student."

输出："student. a am I"

两次reverse翻转

1. reverse()函数翻转整体
2. 快慢指针分割出单词, 再把单词翻转回来

class Solution {
public:
  string reverseWords(string s) {
    reverse(s.begin(), s.end());
    for (int i = 0; i < s.size(); i++) {
      int j = i;
      while (j < s.size() && s[j] != ' ') j++;
      reverse(s.begin() + i, s.begin() + j);  // 前开后闭
      i = j;  // i++后走到空格后
    }
    return s;
  }
};

改编 翻转单词顺序

与上一题不同的是每个单词前后都有数量不定的空格，包括整个句子的前后也可能有一定的空格，如下：

输入: "  hello   world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

代码

class Solution {
public:
  string reverseWords(string s) {
    reverse(s.begin(), s.end());
    int idx = 0, n = s.size();
    for (int start = 0; start < n; start++) {
      if (s[start] != ' ') {
        if (idx != 0) s[idx++] = ' ';
        int end = start;
        while (end < n && s[end] != ' ') s[idx++] = s[end++];
        reverse(s.begin() + idx - (end - start), s.begin() + idx);
        start = end;
      }
    }
    s.erase(s.begin() + idx, s.end());  // s.erase
    return s;
  }
};

左旋转字符串

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。

请定义一个函数实现字符串左旋转操作的功能。

比如输入字符串"abcdefg"和数字 $2$，该函数将返回左旋转 $2$ 位得到的结果"cdefgab"。

注意：

• 数据保证 $n$ 小于等于输入字符串的长度。

数据范围

输入字符串长度 $[0,1000]$。

样例

输入："abcdefg" , n=2

输出："cdefgab"

题解

本质和"翻转句子, 单词不翻转"相同: 把前后两部分看作两个单词。

class Solution {
public:
  string leftRotateString(string str, int n) {
    reverse(str.begin(), str.end());
    reverse(str.begin(), str.end() - n);
    reverse(str.end() - n, str.end());
    return str;  // 报segament fault可能是因为没写return
}
};

Week 7

滑动窗口的最大值★

给定一个数组和滑动窗口的大小，请找出所有滑动窗口里的最大值。

例如，如果输入数组 $[2, 3, 4, 2, 6, 2, 5, 1]$ 及滑动窗口的大小 $3$，那么一共存在 $6$ 个滑动窗口，它们的最大值分别为 $[4, 4, 6, 6, 6, 5]$。

注意：

• 数据保证 $k$ 大于 $0$，且 $k$ 小于等于数组长度。

数据范围

数组长度 $[1,1000]$。

样例

输入：[2, 3, 4, 2, 6, 2, 5, 1] , k=3

输出: [4, 4, 6, 6, 6, 5]

双向单调递减队列

时间复杂度为 $O(n)$, 每个元素都会入队一次, 最多出队一次。

class Solution {
public:
  vector<int> maxInWindows(vector<int>& nums, int k) {
    vector<int> res;
    deque<int> q;  // deque维护滑动窗口(队列), 元素是下标
    for (int i = 0; i < nums.size(); i++) {
      // 保证是递减队列（早进入且小的数字“永无出头之日”）
      while (q.size() && nums[q.back()] <= nums[i]) q.pop_back();
      q.push_back(i);
      if (q.size() && i - q.front() + 1 > k) q.pop_front();
      if (i >= k - 1) res.push_back(nums[q.front()]);
    }
    return res;
  }
};

骰子的点数★

将一个骰子投掷 $n$ 次，获得的总点数为 $s$，$s$ 的可能范围为 $n \sim 6n$。

掷出某一点数，可能有多种掷法，例如投掷 $2$ 次，掷出 $3$ 点，共有 $[1,2],[2,1]$ 两种掷法。

请求出投掷 $n$ 次，掷出 $n \sim 6n$ 点分别有多少种掷法。

数据范围

$1 \le n \le 10$

样例1

输入：n=1

输出：[1, 1, 1, 1, 1, 1]

解释：投掷1次，可能出现的点数为1-6，共计6种。每种点数都只有1种掷法。所以输出[1, 1, 1, 1, 1, 1]。

样例2

输入：n=2

输出：[1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]

解释：投掷2次，可能出现的点数为2-12，共计11种。每种点数可能掷法数目分别为1,2,3,4,5,6,5,4,3,2,1。

      所以输出[1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]。

算法1 dfs暴力递归

不推荐，会存在重复计算状态的问题，会报 TLE(Time Limit Exceeded) 。

时间复杂度: $O(6^n)$

class Solution {
public:
  vector<int> numberOfDice(int n) {
    vector<int> res;
    for (int i = n; i <= 6 * n; i++) res.push_back(dfs(n, i));
    return res;
  }
  
  int dfs(int n, int sum) {
    if (sum < 0) return 0;
    if (!n) return !sum;
    
    int res = 0;
    for (int i = 1; i <= 6; i++) res += dfs(n - 1, sum - i);
    return res;
  }
};

算法2 DP

二维写法

状态表示: f[i][j]表示投掷i次总点数为j的情况数。

class Solution {
public:
  vector<int> numberOfDice(int n) {
    vector<vector<int>> f(n + 1, vector<int>(6 * n + 1, 0));
    f[0][0] = 1;
    for (int i = 1; i <= n; i++) {
      for (int j = i; j <= 6 * i; j++) {
        for (int k = 1; k <= min(j, 6); k++) {
          f[i][j] += f[i - 1][j - k];
        }
      }
    }
    return vector<int>(f[n].begin() + n, f[n].end());
  }
};

一维写法

采用滚动数组优化: 从二维降为一维
注意: 需要清零，比如第3轮[3…18]与第2轮[2…12]有交集[2…12], 计算交集时需要先清除旧值

class Solution {
public:
  vector<int> numberOfDice(int n) {
    vector<int> f(6 * n + 1, 0);
    for (int i = 1; i <= 6; i++) f[i] = 1;
    for (int i = 2; i <= n; i++) {
      for (int j = 6 * i; j >= 0; j--) {
        f[j] = 0;
        for (int k = 1; k <= min(6, j); k++)
          f[j] += f[j - k];
      }
    }
    return vector<int>(f.begin() + n, f.end());
  }
};

扑克牌的顺子

从扑克牌中随机抽 $5$ 张牌，判断是不是一个顺子，即这 $5$ 张牌是不是连续的。

$2 \sim 10$ 为数字本身，$A$ 为 $1$，$J$ 为 $11$，$Q$ 为 $12$，$K$ 为 $13$，大小王可以看做任意数字。

为了方便，大小王均以 $0$ 来表示，并且假设这副牌中大小王均有两张。

样例1

输入：[8,9,10,11,12]

输出：true

样例2

输入：[0,8,9,11,12]

输出：true

模拟法

顺子条件：

1. 除0外无重复数字
2. 用0能把空位填上，使之成为连续数字

算法步骤：

1. 排序
2. 删0
3. 判断有无重复
4. 看最大值与最小值的差距是否小于等于4

class Solution {
public:
  bool isContinuous(vector<int> nums) {
    if (nums.empty()) return false;
    
    sort(nums.begin(), nums.end());
    int k = 0;
    while (nums[k] == 0) k++;
    for (int i = k + 1; i < nums.size(); i++) {
      if (nums[i] == nums[i - 1])
        return false;
    }
    return nums.back() - nums[k] <= 4;
  }
};

圆圈中最后剩下的数字★

$0, 1, …, n-1$ 这 $n$ 个数字 $(n>0)$ 排成一个圆圈，从数字 $0$ 开始每次从这个圆圈里删除第 $m$ 个数字。

求出这个圆圈里剩下的最后一个数字。

数据范围

$1 \le n,m \le 4000$

样例

输入：n=5 , m=3

输出：3

约瑟夫环问题

采用递归方法解决此问题, 旧坐标系中f(n, m)问题转化为新坐标系f(n - 1, m)问题
新坐标系起点 在 旧坐标系中下标为m, 因此点在旧坐标系中坐标 = (在新坐标系中坐标 + m) % n

时间复杂度为 $ O(n)$

class Solution {
public:
  int lastRemaining(int n, int m){
      if (n == 1) return 0;
      return (lastRemaining(n - 1, m) + m) % n;
   }
};

股票的最大利润★

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖 一次 该股票可能获得的利润是多少？

例如一只股票在某些时间节点的价格为 $[9, 11, 8, 5, 7, 12, 16, 14]$。

如果我们能在价格为 $5$ 的时候买入并在价格为 $16$ 时卖出，则能收获最大的利润 $11$。

数据范围

输入数组长度 $[0,500]$。

样例

输入：[9, 11, 8, 5, 7, 12, 16, 14]

输出：11

模拟法

如何枚举: 以哪天卖出进行枚举
如何求前i天的最小值: 维护一个变量minv记录前i天的最小进价

class Solution {
public:
  int maxDiff(vector<int>& nums) {
    if (nums.empty()) return 0;
    int res = 0, minv = nums[0];  // 最低进价初始化为nums[0], 而非0
    for (int i = 0; i < nums.size(); i++) {
      res = max(res, nums[i] - minv);
      minv = min(minv, nums[i]);
    }
    return res;
  }
};

求1+2+…+n★

求 $1+2+…+n$，要求不能使用乘除法、$for$、$while$、$if$、$else$、$switch$、$case$ 等关键字及条件判断语句 $(A?B:C)$。

数据范围

$1 \le n \le 50000$。

样例

输入：10

输出：55

语法题

class Solution {
public:
  int getSum(int n) {
    n > 0 && (n += sumNums(n - 1));
    return n;
  }
};

不用加减乘除做加法★

写一个函数，求两个整数之和，要求在函数体内不得使用 $＋、－、×、÷$ 四则运算符号。

数据范围

$-1000 \le num1,num2 \le 1000$

样例

输入：num1 = 1 , num2 = 2

输出：3

算法

思路

1) 全加器的实现
    A   A 0 1 0 1
+   B   B 0 0 1 1
-----   C 0 1 1 0  
  C D   D 0 0 0 1
即
C = A ^ B        异或
D = (A & B) << 1 与, 左移1位
运算可并行计算

2) A + B = sum + carry, 并且循环可结束. 结束时carry=0, sum = A + B
若num1 & num2结果末尾中有k个0, 则num2 = (num1 & num2) << 1末尾有k+1个0
下一次循环中(num1 & num2) << 1至少有k+2个0, ...

代码

class Solution {
public:
  int add(int num1, int num2){
    int sum, carry;
    while (num2) {
      sum = num1 ^ num2;
      carry = (num1 & num2) << 1;
      num1 = sum;
      num2 = carry;
    }
    return sum;
  }
};

构建乘积数组★

给定一个数组A[0, 1, …, n-1]，请构建一个数组B[0, 1, …, n-1]，其中B中的元素B[i]=A[0]×A[1]× … ×A[i-1]×A[i+1]× … ×A[n-1]。

不能使用除法。

数据范围

输入数组长度 $[0,20]$。

样例

输入：[1, 2, 3, 4, 5]

输出：[120, 60, 40, 30, 24]

思考题：

• 能不能只使用常数空间？（除了输出的数组之外）

曲线救国

class Solution {
public:
  vector<int> multiply(const vector<int>& A) {
    if (A.empty()) return vector<int>();
    int n = A.size();
    vector<int> B(n);
    
    // B[i] = (A[0]×A[1]×… ×A[i-1]) × (A[i+1]×…×A[n-1]), 曲线救国, 分两步走
    // 此循环中p记录的是B[i]左半部分乘积
    for (int i = 0, p = 1; i < n; i++) {
      B[i] = p;
      p *= A[i];
    }
    
    // 此循环中p记录的是B[i]右边部分乘积
    for (int i = n - 1, p = 1; i >= 0; i--) {
      B[i] *= p;
      p *= A[i];
    }
    return B;
  }
};

把字符串转换成整数

请你写一个函数 StrToInt，实现把字符串转换成整数这个功能。

当然，不能使用 atoi 或者其他类似的库函数。

数据范围

输入字符串长度 $[0,20]$。

样例

输入："123"

输出：123

注意:

你的函数应满足下列条件：

1. 忽略所有行首空格，找到第一个非空格字符，可以是 ‘+/−’ 表示是正数或者负数，紧随其后找到最长的一串连续数字，将其解析成一个整数；
2. 整数后可能有任意非数字字符，请将其忽略；
3. 如果整数长度为 $0$，则返回 $0$；
4. 如果整数大于 INT_MAX($2^{31} − 1$)，请返回 INT_MAX；如果整数小于INT_MIN($−2^{31}$) ，请返回 INT_MIN；

题解

class Solution {
public:
  int strToInt(string str) {
    int k = 0;
    while (k < str.size() && str[k] == ' ') k++;
    
    bool is_minus = false;
    if (str[k] == '+') {
      k++;
    } else if (str[k] == '-') {
      is_minus = true;
      k++;
    }
    
    long long num = 0;
    while (k < str.size() && str[k] >= '0' && str[k] <= '9') {
      num = 10 * num + str[k] - '0';
      if (num > INT_MAX) break;
      k++;
    }
    if (is_minus) num *= -1;
    if (num > INT_MAX) return INT_MAX;
    if (num < INT_MIN) return INT_MIN;
    return num;
  }
};

树中两个结点的最低公共祖先★

给出一个二叉树，输入两个树节点，求它们的最低公共祖先。

一个树节点的祖先节点包括它本身。

注意：

• 输入的二叉树不为空；
• 输入的两个节点一定不为空，且是二叉树中的节点；

数据范围

树中节点数量 $[0,500]$。

样例

二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]如下图所示：
    8
   / \
  12  2
     / \
    6   4

1. 如果输入的树节点为2和12，则输出的最低公共祖先为树节点8。

2. 如果输入的树节点为2和6，则输出的最低公共祖先为树节点2。

递归法

lowestCommonAncestor返回值意义

1. 若p,q都属于Tree, 则返回最低公共祖先
2. 若只有一方(如p)属于Tree, 则返回p
3. 若两者都不属于Tree, 则返回null

时间复杂度为 $O(n)$: 每个点最多遍历一次

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (!root) return nullptr;
    if (root == p || root == q) return root;
    auto left = lowestCommonAncestor(root->left, p, q);
    auto right = lowestCommonAncestor(root->right, p, q);
    if (left && right) return root;
    if (left) return left;
    return right;
  }
};