论文： Y, Zhang X, Wang L. Asymmetrical vertical federated learning[J]. arXiv preprint arXiv:2004.07427, 2020.

在联邦学习中，通常会使用基于ID的样本对齐方法，但却很少关注保护ID的隐私。为了缓解对于ID隐私的担忧，本文正式提出非对称纵向联邦学习的概念，并且阐述了保护样本ID的方法。
标准的隐私求交通常在非对称纵向联邦学习的样本对齐阶段被采用，本文相应的提出了一种 Pohlig-Hellman 实现机制。本文还提出了一种 真正的虚拟(genuine with dummy) 方法来实现非对称联邦学习训练。

Introduction

在联邦学习中，尤其是在纵向场景中，在利用ID对齐分布数据集后，忽略样本的D信息泄露是常见但是不合理的。实际应用中，参与方通常是具有"页面没有找到"司或者机构，因此，一方面，参与者不允许披露它们的样本ID；另一方面，现实生活中存在着不对称的联邦，其中一部分参与者是对ID隐私要求很高的小公司，而另一部分是对ID隐私不太关心的大公司(交集一旦公布，小公司的ID隐私泄露很严重，考虑极端情况，甚至会完全泄露)。这种不平衡的设置需要一个纵向联邦学习系统来区分联邦的”强“和“弱”侧，并且考虑到他们特定的隐私保护需求。

本文将纵向联邦学习分为对称型和非对称型，以便设计保护ID的联邦学习算法。本文的贡献包括：

  1. 提出非对称纵向联邦学习的概念。

  2. 吸收标准隐私求交协议以在非对称联邦学习系统中实现非对称ID对齐。此外，我们提供一种Pohlig-Hellman的适配隐私求交的实现。

  3. 我们提出了一种真正的虚拟方法以实现不对称的联邦模型训练。为了展示其应用，提供联邦逻辑回归算法作为例子。

Problem Definition

Vertical Federated Learning

使用 D=(I,X,Y)\mathcal{D}=(\mathcal{I,X,Y}) 表示1个完整的数据集，其中 D,X,Y\mathcal{D,X,Y} 分别表示样本ID空间、特征空间和标签空间。纵向联邦学习被定义为在2个数据集 D1=(I1,X1,Y1)\mathcal{D}_1=(\mathcal{I}_1,\mathcal{X}_1,\mathcal{Y}_1) 和 D2=(I2,X2,Y2)\mathcal{D}_2=(\mathcal{I}_2,\mathcal{X}_2,\mathcal{Y}_2) 上，这2个数据集满足：

X1≠X2,Y1≠Y2,I1=I2\mathcal{X}_{1} \neq \mathcal{X}_{2}, \mathcal{Y}_{1} \neq \mathcal{Y}_{2}, \mathcal{I}_{1}=\mathcal{I}_{2}

然而在现实应用中，几乎无法找到2个共享相同ID空间的数据集。因此，在纵向联邦学习的预处理阶段有必要引入ID对齐（ID-alignment）协议，以帮助各方安全识别交集 I1=I2\mathcal{I}_1=\mathcal{I}_2 并建立两个数据集的行映射。

我们定义 D1o=(I1o,X1,Y1)，D2o=(I2o,X2,Y2)\mathcal{D}_{1}^{o}=\left(\mathcal{I}_{1}^{o}, \mathcal{X}_{1}, \mathcal{Y}_{1}\right)，\mathcal{D}_{2}^{o}=\left(\mathcal{I}_{2}^{o}, \mathcal{X}_{2}, \mathcal{Y}_{2}\right) 为关于 D1,D2\mathcal{D}_1,\mathcal{D}_2 的待对齐（pre-ID-alignment）数据集，满足 I1∈I1o,I2∈I2o\mathcal{I}_1\in\mathcal{I}_1^o,\mathcal{I}_2\in\mathcal{I}_2^o（Iio\mathcal{I}_i^o为对齐前的数据集对应的样本空间）。此外，我们使用 IwI^w 表示完整的ID空间，其包含 D1o\mathcal{D}_1^o 和 D2o\mathcal{D}_2^o 中的所有可能的元素。

Private Set Intersection

在标准隐私求交(PSI)中，每一个参与方 Pi\mathcal{P}_i 拥有一个包含所有机密数据的数据集SiS_i。所有的参与方会协作求出交集S′=∩iSiS^\prime=\cap_i{S_i}，与此同时每一参与方 Pi\mathcal{P}_i 保持 Si/S′S_i / S^\prime 私有。PSI的实现方法可以基于：

  • 传统的公钥密码体系
  • 不经意传输
  • 混淆电路

Symmetrical and Asymmetrical

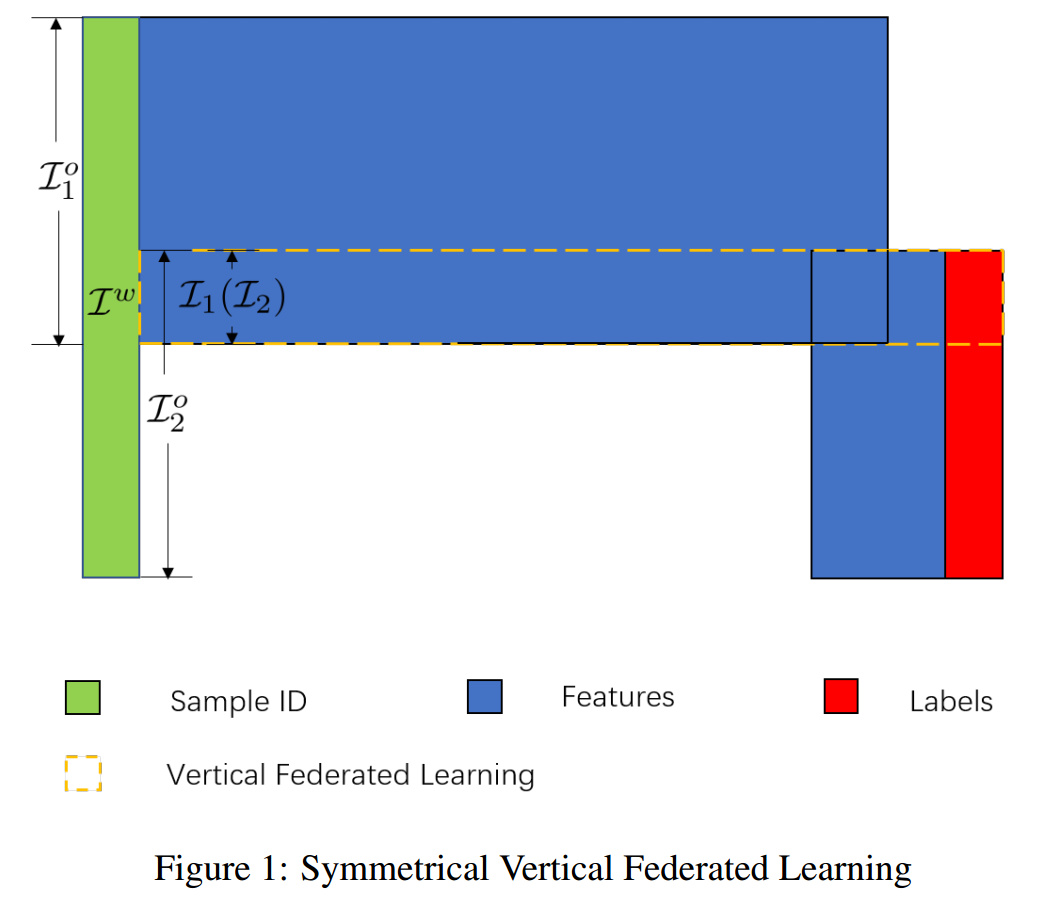
在上面的图1中，P1\mathcal{P}_1 和 P2\mathcal{P}_2 就待对齐样本的元素数量上拥有同等的地位。事实上，即使P1\mathcal{P}_1随机选择 e∈Iwe\in \mathcal{I}^w，也会有 ∣I2o∣/∣Iw∣≫0\left|\mathcal{I}_{2}^{o}\right| /\left|\mathcal{I}^{w}\right| \gg 0 的概率选到 e∈Iwe\in \mathcal{I}^w。在这种"强联邦（federation of the strong）"中，每一方都不会在执行PSI协议求交集 I1=I2\mathcal{I}_1=\mathcal{I}_2 的过程中掌握很多的信息，因此也不会让对方知道自己很多的ID信息，本文称这种方案为对称纵向联邦学习（Symmetrical Vertical Federated Learning，SVFL）。

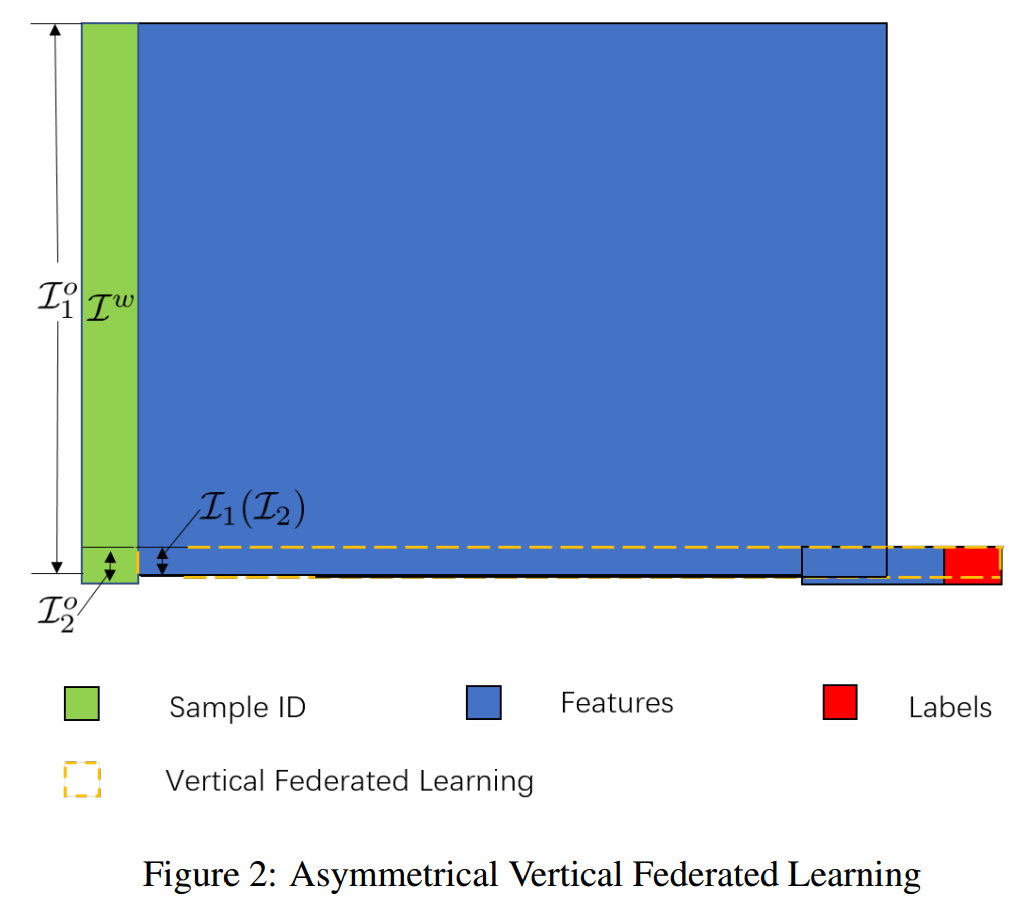
与SVFL相反的情况是 P2\mathcal{P}_2 有 ∣I2o∣/∣Iw∣≈0\left|\mathcal{I}_{2}^{o}\right| /\left|\mathcal{I}^{w}\right| \approx 0，而 P1\mathcal{P}_1 中有 ∣I1o∣/∣Iw∣≫0\left|\mathcal{I}_{1}^{o}\right| /\left|\mathcal{I}^{w}\right| \gg 0。

一种常见的情况是，建立的联邦学习是 P2\mathcal{P}_2 的学习任务。纵向联邦数据分布如图2所示， P2\mathcal{P}_2 是联邦学习中的弱方（weak side），因为 P2o\mathcal{P}_2^o 中每个样本的ID都被视为敏感数据，也就是说在求交 I1=I2\mathcal{I}_1=\mathcal{I}_2 的过程中其隐私会被严重危害。在这种强弱联邦（federation of the weak and the strong）中，有必要在ID对齐阶段保护弱方的ID隐私，这种方案称为非对称纵向联邦学习（Asymmetrical Vertical Federated Learning, AVFL）。

不考虑弱联邦（federation of the weak），因为我们可以通过将全空间 Iw\mathcal{I}^w 缩减为 Iw\(I1o∪I2o)\mathcal{I}^{w} \backslash\left(\mathcal{I}_{1}^{o} \cup \mathcal{I}_{2}^{o}\right) ，从而将”弱联邦“转化为“强联邦”。

（没看懂弱联邦说的是啥）

假设1：Iw=I10∪I2o\mathcal{I}^w=\mathcal{I}^0_1\cup \mathcal{I}_2^o

定义1：

  1. 如果满足以下条件，则称为 Symmetrically Vertical Federated Learning(SVFL)：

−12≤log⁡10∣I1o∣∣Iw∣,log⁡10∣I1o∣∣Iw∣≤0-\frac{1}{2} \leq \log _{10} \frac{\left|\mathcal{I}_{1}^{o}\right|}{\left|\mathcal{I}^{w}\right|}, \log _{10} \frac{\left|\mathcal{I}_{1}^{o}\right|}{\left|\mathcal{I}^{w}\right|} \leq 0

  1. 如果以下两个条件中任意一个等式成立，都可以称为``Asymmetrical Vertical Federated Learning(AVFL)` ：

    log⁡10∣I1o∣∣Iw∣<−12log⁡10∣I2o∣∣Iw∣<−12\begin{array}{l} \log _{10} \frac{\left|\mathcal{I}_{1}^{o}\right|}{\left|\mathcal{I}^{w}\right|}<-\frac{1}{2} \\ \log _{10} \frac{\left|\mathcal{I}_{2}^{o}\right|}{\left|\mathcal{I}^{w}\right|}<-\frac{1}{2} \end{array}

    如果上面的条件成立，P1\mathcal{P}_1 可称为弱方，P2\mathcal{P}_2 称为强方。
    分析：由上面的条件可以得到∣I1o∣∣Iw∣<1012≈0.316\frac{\left|\mathcal{I}_{1}^{o}\right|}{\left|\mathcal{I}^{w}\right|}<10^{\frac{1}{2}}\approx 0.316，即样本数量占比低于0.316的为弱方。

    以上的分析都是两方的，事实上，通过非对称保护弱方的样本ID隐私，可以将分析简单扩展到多方案例。

Asymmetrical ID Alignment

ID对齐是纵向联邦学习工作流的第一步。本节中，我们采用标准PSI协议以实现非对称ID对齐，并提供了一种使用传统密码学的实现方法。

Asymmetrical PSI Protocols

在SVFL的样本对齐阶段，标准PSI协议的执行不仅让各方获得共有样本的知识，还提供了一个标签，可以有效地将分布式样本片段链接在一起，为后续的联邦学习铺平道路。而在AVFL中，为了正确实现样本对齐，必须采取满足如下条件的标准PSI协议：

  1. 真实交集 I1=I2\mathcal{I}_1=\mathcal{I}_2 对强参与方保密
  2. 在联邦模型训练阶段， I1=I2\mathcal{I}_1=\mathcal{I}_2 对应的分布式样本仍然可以对齐

使用 Iwo\mathcal{I}_{w}^{o} 和 Iso\mathcal{I}_{s}^{o} 分别表示待ID对齐的弱方和强方的样本ID集合，二者定义如下：

{Iwo}=argmin⁡I∈{I1o,I2o}∣I∣,{Iso}=argmax⁡I∈{I1o,I2o}∣I∣.\left\{\mathcal{I}_{w}^{o}\right\}=\underset{\mathcal{I} \in\left\{\mathcal{I}_{1}^{o}, \mathcal{I}_{2}^{o}\right\}}{\operatorname{argmin}}|\mathcal{I}|,\left\{\mathcal{I}_{s}^{o}\right\}=\underset{\mathcal{I} \in\left\{\mathcal{I}_{1}^{o}, \mathcal{I}_{2}^{o}\right\}}{\operatorname{argmax}}|\mathcal{I}| .

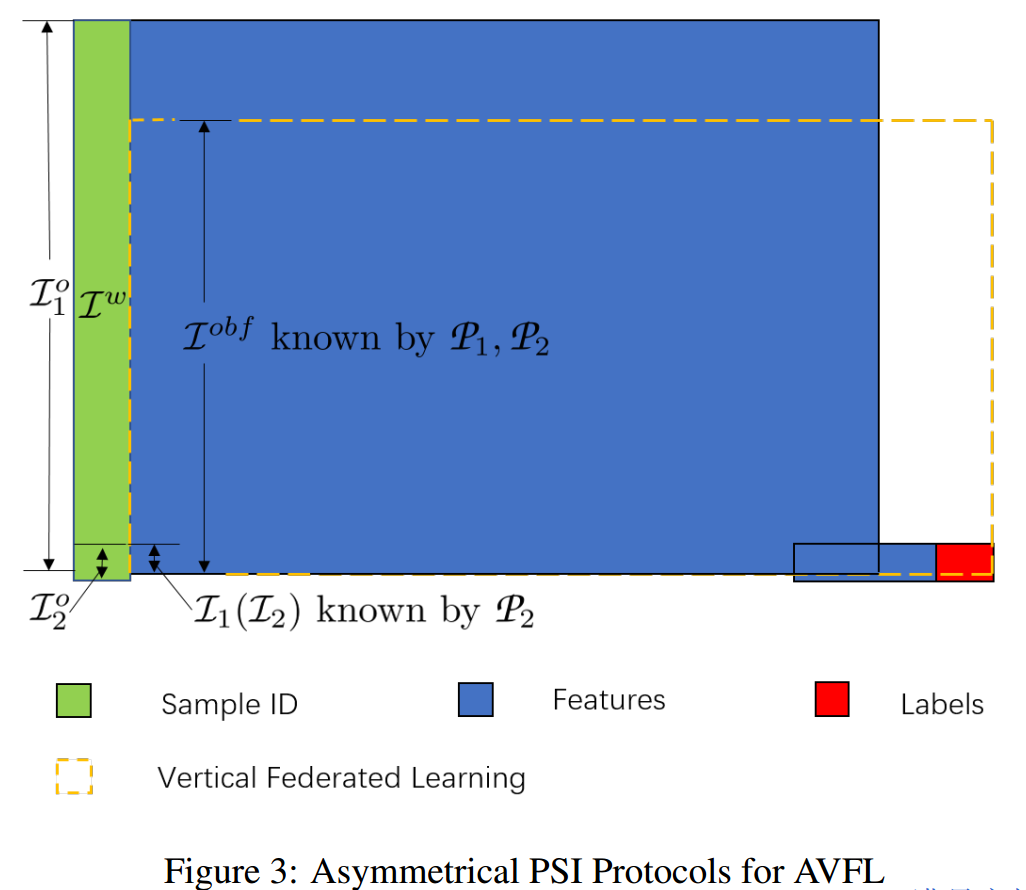
定义2：非对称PSI（Asymmetrical PSI，APSI）协议会在双方产生一个扰动集合 Iobf⊂Iso\mathcal{I}^{o b f} \subset \mathcal{I}_{s}^{o} ，满足：

I1=I2⊂Iobf⊂Iso\mathcal{I}_{1}=\mathcal{I}_{2} \subset \mathcal{I}^{o b f} \subset \mathcal{I}_{s}^{o}

此外，弱方会知道真实交集 I1=I2\mathcal{I}_1=\mathcal{I}_2。

APSI协议的结果如图3所示：

A Pohlig-Hellman Realization

使用Gn=(Zn∗,⋅)G_n=(\mathbb{Z}_n^*, \cdot)表示一个乘法群，而后 Pohlig-Hellman加密体制可以用以下3个组件进行描述：

  1. (Key generation) 选择1个素数 pp 使得每一个明文元素都是 GpG_p 中的一个元素，并且 p−1p-1有至少1个大素数因子。然后选择 a∈Gp−1a\in G_{p-1} 并计算 a−1∈Gp−1a^{-1}\in G_{p-1}。最后，一方展示 GpG_p 作为公共知识，并将(a,a−1)(a, a^{-1})作为对称密码体系的密钥。

  2. (Encryption) 加密明文m∈Gpm\in G_p为：

    Ea(m)=maE_a(m)=m^a

  3. (Decryption) 解密密文c∈Gpc\in G_p为：

    Da(c)=ca−1D_a(c)=c^{a^{-1}}

Pohlig-Hellman加密体制满足交换律，也就是说：∀a,b∈Gp−1,Ea∘Eb=Eb∘Ea\forall a,b\in G_{p-1},E_{a} \circ E_{b}=E_{b} \circ E_{a}。（“先用a加密再用b加密“和”先用b加密再用a加密“的密文相同）。基于Pohlig-Hellman加密的APSI协议如算法1所示：

其中，Ii\mathrm{I_i} 表示的是ID的明文，Ui\mathrm{U}_i 表示的加密1次的密文，Ui†\mathrm{U}_i^\dagger 为加密2次的密文。

协议思想较为简单，核心在于第7步中，P2\mathcal{P}_2 会随机选择出U1†∩U2†⊂Uobf†⊂U1†\mathrm{U}_{1}^{\dagger} \cap \mathrm{U}_{2}^{\dagger} \subset \mathrm{U}^{o b f \dagger} \subset \mathrm{U}_1^\dagger ，Uobf†\mathrm{U}^{obf\dagger}对应的明文除了包含真正的交集外还包含 I1\mathrm{I}_1 中的部分数据，但 I1o∩I2o=I2o∩Iobf=I1=I2\mathcal{I}_1^o\cap \mathcal{I}_2^o =\mathcal{I}_{2}^{o} \cap \mathcal{I}^{obf}=\mathcal{I}_1=\mathcal{I}_2 的是后续求交运算准确性的基础。

注意：安全数（secure number）λ\lambda被解释为模糊交集 Iobf\mathcal{I}^{obf} 与真实交集 I1=I2\mathcal{I}_1=\mathcal{I}_2 的基数比 h(λ)h(\lambda) ，详细作用可看算法1。

也就是说从模糊交集中随机选择一元素，其恰好位于真实交集的概率为 1/h(λ)1/h(\lambda) 。进一步地，h(0)=1h(0)=1 表示的是模糊交集与真实交集完全相同，P1,P2\mathcal{P}_1,\mathcal{P}_2 拥有的全都是真实交集，即这种特殊情况下AVFL变成了SVFL。而 λ=1\lambda=1 时对应的，Iobf=I1\mathcal{I}^{obf}=\mathcal{I}^1，此时 P1\mathcal{P}_1 无法从算法1中获取任何信息。
随着 λ\lambda 从0递增到1，1/h(λ)1/h(\lambda) 指数递减，因此 P1\mathcal{P}_1 更难从模糊交集中分辨出真实交集，更安全。

Asymmetrical Federated Model Training

Genuine with Dummy Approcah

如图3所示，纵向联邦学习学习域中现在包含有空白（margin），也就是说在 Iobf/ I1\mathcal{I}^{obf}/\ \mathcal{I}_1 对应的样本缺少全部的标签和部分特征。虽然联邦迁移学习中可以通过特征表示迁移（ feature-representation-transfer）方法填充这些空白，但是在现实很多应用中，比如金融风险管控中更倾向于选择少量但准确的原始数据。

因此，有必要设计能够使用APSI协议产生的分布式结构作为输入，但是产生与SVFL相同结果的非对称模型训练协议。本文展示了一种带虚拟的真实（Genuine with Dummy，GWD）方法以实现非对称模型训练。注意此处需要引入可行第三方 P3\mathcal{P}_3；

  1. P3\mathcal{P}_3 产生1个公钥密码系统，将公钥分发给 P1\mathcal{P}_1 和 P2\mathcal{P}_2
  2. P1\mathcal{P}_1 与 P2\mathcal{P}_2 交换中间变量以协作地计算梯度和损失。 弱方 P2\mathcal{P}_2 将会在真实交集中的数据样本上正常执行运算规则，而在虚拟样本执行数学恒等式运算，以便它们的存在不会影响相关计算结果
  3. P1\mathcal{P}_1 与 P2\mathcal{P}_2 将数据分发给 P3\mathcal{P}_3 以完成梯度和损失的解密，并完成局部模型的更新

为了让强方不知道虚拟样本的存在，一种可行的方式是实现语义安全的加密方案，比如Paillier同态加密。此外，因为引入的恒等式严格保证每一步的中间结果不变，使用GWD方法实现的非对称模型训练将表现出与标准（对称）模型训练方案相同的性能。

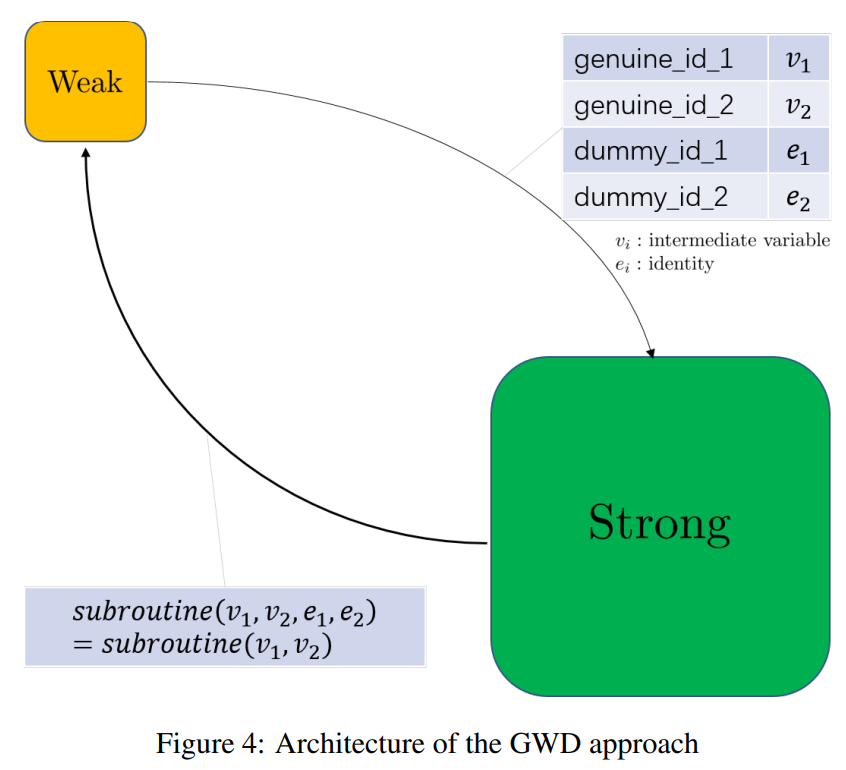
图4展示了GWD架构，其展示了一个通用子例程的联邦执行过程。弱方将会发送密文消息 v1,v2v_1,v_2 给强方，然后等待来自强方关于 subroutine(v1,v2)subroutine(v_1,v_2) 的执行结果 。由于直接传输会泄露真实ID信息。因此，弱方在发送 v1,v2v_1,v_2 的同时会加上关于虚假样本的数学等价符 e1,e2e_1,e_2 ，最终会收到 subroutine(v1,v2,e1,e2)=subroutine(v1,v2)subroutine(v_1,v_2,e_1,e_2)= subroutine(v_1,v_2)。此外，强方会运算 subroutine(⋅)subroutine(\cdot) ， 而不会察觉真实ID。

（没看懂得1和2的关系，以及为啥要加e）

Asymmetrical Vertical Logistic Regression

不妨先看看Shengwen Yang, Bing Ren, Xuhui Zhou, and Liping Liu. Parallel distributed logistic regression for vertical federated learning without third-party coordinator. arXiv preprint arXiv:1911.09824, 2019.中的无协调者的纵向联邦逻辑回归训练方案：

Party A 拥有 xA,ΘA,yx_{A}, \Theta_{A}, y，而Party B 拥有 xB,ΘBx_{B}, \Theta_{B}，这些数据都是不能直接明文传输的。

Step 3 中Party A 向 Party B传输同态密文[ ⁣[(yi−yi^)] ⁣][\![(y_i-\hat{y_i})]\!] 的原因在于明文的**(yi−yi^)(y_i-\hat{y_i}) 在分类任务中会泄露信息**，由于0≤yi^≤10\le\hat{y_i}\le1，真实标签yi=0y_i=0 则式子为负数，yi=1y_i=1 则对应式子为正数。补充：这在梯度泄露攻击中是一种常用的恢复真实标签的方法。

（不明白计算机是怎么计算梯度的，仅利用加法同态就能计算出梯度？）

接着再看以无协调者的纵向联邦逻辑回归训练为基础，使用GWD方法将其调整为不对称的训练协议，然后使用算法2中提出的非对称纵向逻辑回归（AVLR）训练协议进行训练。（注意：P1\mathcal{P}_1 对应上表中的Party A，而 P2\mathcal{P}_2 对应上表中的Party B）

对于存在于I1o/(I1∩I2)I_1^o/(I_1 \cap I_2) 的样本，这里的处理核心在于第5步：由于P2\mathcal{P_2} 知道哪些样本仅在I1∩I2I_1\cap I_2 中，哪些样本是添加的混淆样本，因此他可以直接把来自I1o/(I1∩I2)I_1^o/(I_1 \cap I_2) 的样本对应的损失设置为0进行处理。

算法2的核心在于第5、6步中让弱方P2\mathcal{P}_2 共享加密的标量（scalars）⟨ϕik⟩\left\langle\phi_{i k}\right\rangle，以便让P1\mathcal{P}_1 计算出加密的本地梯度⟨∇sL(wk)⟩\left\langle\nabla^{s} \mathcal{L}\left(\mathbf{w}_{k}\right)\right\rangle，标量⟨ϕik⟩\left\langle\phi_{i k}\right\rangle 的提出直接体现了GWD的思想。

P1\mathcal{P}_1 会在 Ikobf\mathcal{I}_k^{obf} 对应的样本上计算梯度 ⟨∣I1o∩I2o∣⋅∇sL(wk)⟩=∑ei∈Iobf⟨ϕik⟩xis\left\langle\left|\mathcal{I}_{1}^{o} \cap \mathcal{I}_{2}^{o}\right| \cdot \nabla^{s} \mathcal{L}\left(\mathbf{w}_{k}\right)\right\rangle=\sum_{e_{i} \in \mathcal{I}^{o b f}}\left\langle\phi_{i k}\right\rangle \mathbf{x}_{i}^{s}，注意对应明文的系数为 ∣I1o∩I2o∣|\mathcal{I}_1^o\cap\mathcal{I}_2^o|，虽然 P1\mathcal{P}_1 不知道系数（即其连交集结果的基数cardinality都不知道），但是这个除系数的操作是通过将密文发送给 P2\mathcal{P}_2 ，让其在掩码下完成除系数操作。

这里是通过哈达玛乘积（Hadamard Product）添加掩码的，Hadamard Product是一种对两同型矩阵进行的运算：

(A∘B)ij=(A)ij(B)ij(A \circ B)_{i j}=(A)_{i j}(B)_{i j}

即是逐元素添加模乘的掩码。由于明文运算的需要，这里只能添加模乘掩码，不能添加模加掩码，掩码的本质是一次一密，模加和模乘都可以，但这里计算输出时是需要消除掩码的，为了消除模乘的掩码，操作需要在域上进行操作（不能仅仅是环）。

Experiments

实验将验证APSI+AVLR协议的可行性，并与对称型协议进行对比。

Settings

  • 框架：FATE

  • 硬件：两方都使用4核心，16 GB RAM的腾讯云服务器

  • 数据集：MNIST——60000个样本，每个样本784个特征（输入的像素）

    处理方式：手工为每一个样本分配一个ID，划分和分配的规则如下表所示：

联邦训练将会在 P1\mathcal{P}_1 和 P2\mathcal{P}_2 共有的10000个样本上进行（因此，预计训练性能不如其他将整个数据集作为输入的算法，但不影响验证和比较）。

Numerical Results

超参数设置：学习率 η=0.15\eta=0.15，迭代次数=150=150

不断增加安全数（security numbers），即λ=0, 0.25, 0.5, 0.75, 1\lambda=0,\ 0.25,\ 0.5,\ 0.75,\ 1 分别进行测试，记录各种情况下训练的损失和AUC，并绘制出模糊轨迹图：

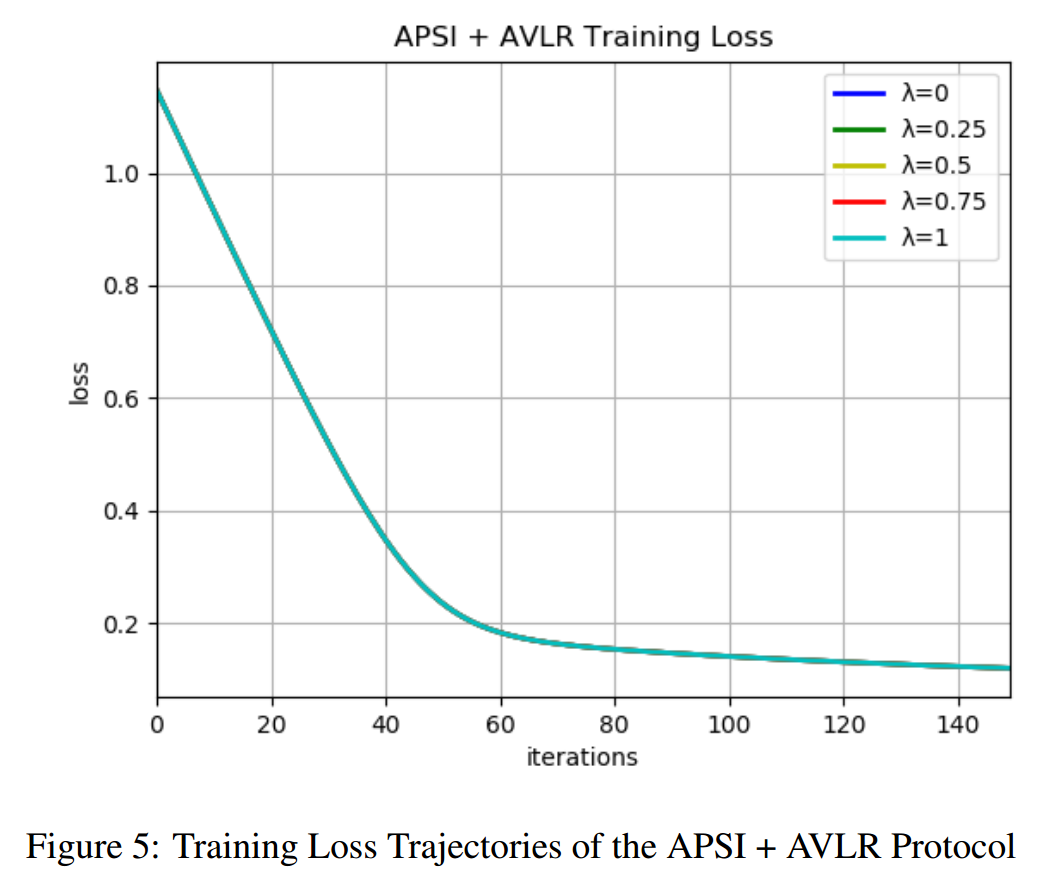
由图5可见，训练的损失不随安全数 λ\lambda 变化而变化。注意：λ=0\lambda=0 对应的对称型 和λ=1\lambda= 1对应的Iobf=Iio\mathcal{I}^{obf}=\mathcal{I}_i^o 的情况对应的训练损失表现是相同的。

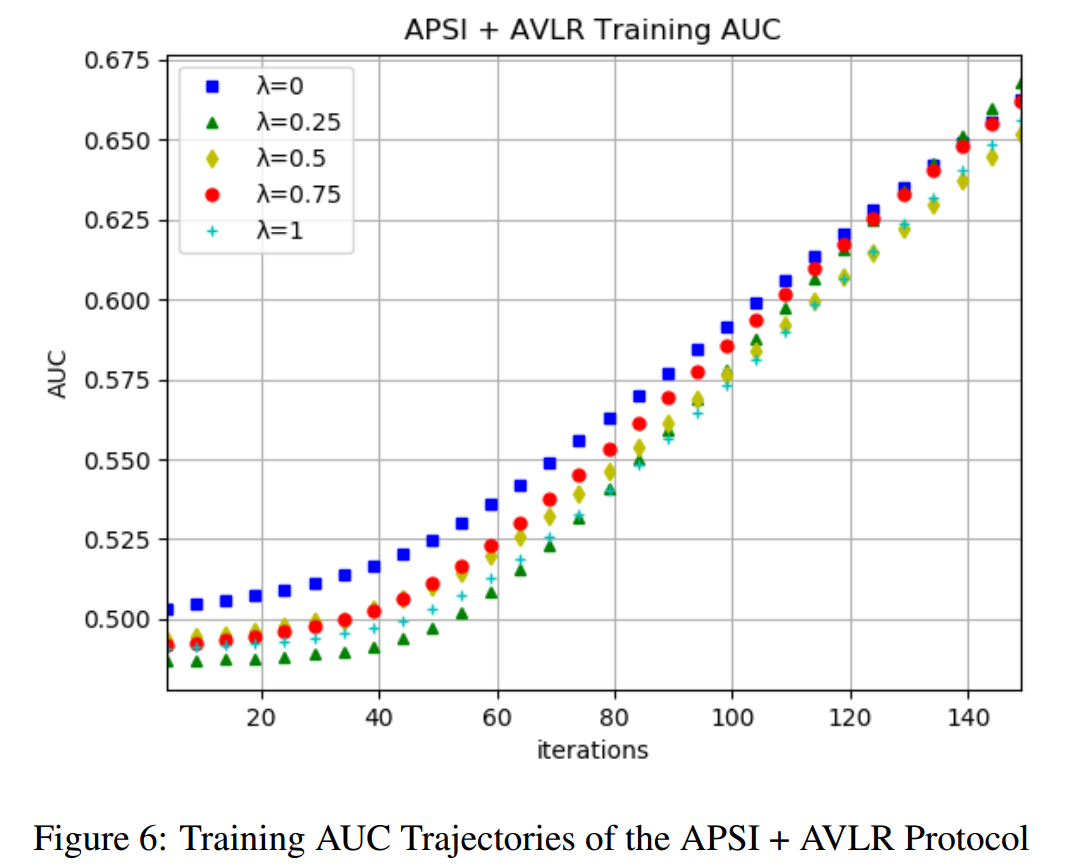
[AUC](如何理解机器学习和统计中的AUC？ - 无涯的回答 - 知乎 https://www.zhihu.com/question/39840928/answer/241440370)是一个用于评价二分类模型的模型评价指标，为ROC曲线下的图形面积。

（不清楚MNIST对应的并不为二分类问题，不知道为啥能用）

由图6可见，不同λ\lambda 对应的AUC曲线的趋势相近。

实验验证：在引入数学恒等式的概念后，APSI+AVLR协议拥有与对称纵向联邦学习拥有相同的表现。